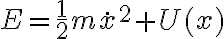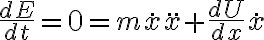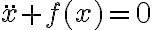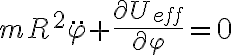MecNew: Parcial 2018 ejercicio 1.c

Buenas. Yo en este ejercicio uso el potencial efectivo de la ecuación de movimiento (ya que la derivada primera de tita no aparece en la misma) y me queda que es : -sen(θ).K/m. por lo que la derivada de eso me quedaría: -cos(θ).K/m. Pero cuando lo evalúo en los puntos θ = 0 y θ = pi/2 me dan cambiadas las estabilidades. Qué estaría haciendo mal? Porque no le encuentro la vuelta. Saludos

Re: Parcial 2018 ejercicio 1.c

de Nicolás Casaballe - domingo, 9 de mayo de 2021, 18:36

Hola, Lucas. Hay que tener cuidado que, al escribir la ecuación de movimiento, la parte que identificamos como «potencial efectivo» depende de cómo esté escrita.

Hagamos un poco de 'ingeniería inversa'. Supongamos que tenemos un problema en una dimensión con una coordenada 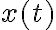$x(t)$ y que encontramos que la cantidad

$E = \frac 1 2 m \dot x^2 + U(x)$

se mantiene constante durante el movimiento. Entonces podemos calcular la derivada con respecto al tiempo:

$\dfrac {dE}{dt} = 0 = m \dot x \ddot x + \dfrac {dU}{dx} \dot x$

donde usé la regla de la cadena para derivar 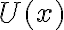$U(x)$ respecto al tiempo. Ya que no nos interesa la solución trivial 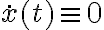$\dot x(t) \equiv 0$ para todo tiempo, cancelamos este término y, dividiendo por la masa, queda

$\ddot x + \dfrac 1 m \dfrac {dU }{dx} = 0$

Esto lo tenemos que comparar con la ecuación de movimiento que puede ser obtenida por otros métodos. Supongamos que es posible usar cierta función 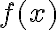$f(x)$ para escribir la ecuación de movimiento como

$\ddot x + f(x) = 0$

Entonces, podemos identificar que el último término es

$f(x) = \dfrac 1 m \dfrac {dU }{dx} = 0$

(si hacemos el proceso de abajo hacia arriba, estamos 'preintegrando').

------

Revisá si en tu planteo del ejercicio del parcial estás haciendo la identificación correcta (con la variable angular, claro).

------

Una cuestión extra que puede ayudar a conectar todo esto es comparar con la ecuación de movimiento de un sencillo sistema de masa resorte:

$m\ddot x = -kx \quad \leftrightarrow \quad \ddot x + \dfrac k m x = 0$

En este caso vemos que 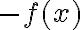$-f(x)$ es ni más ni menos que la fuerza elástica dividida por la masa. Sabemos que el signo de esta fuerza es contrario al de x, y que hay un punto de equilibrio estable en 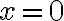$x=0$ . Podemos razonar por analogía en problemas más complicados!!

-------

Saludos,
NC

Re: Parcial 2018 ejercicio 1.c

de Ricardo Marotti - domingo, 9 de mayo de 2021, 18:56

Estimado:

Las posiciones de equilibrio relativo en este ejercicio son 0 y

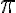$\pi$ (no

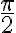$\frac{ \pi }{2}$ ). Y no sé de dónde obtuviste esa energía potencial pero no es correcta. Eso que escribís vos es la aceleración angular

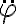$\ddot{ \varphi }$ , que no es la energía potencial efectiva.

La energía potencial efectiva (para la frecuencia angular dada) es:

$- k R^2 cos \varphi$

a menos de una constante. Para obtenerla tenés que preintegrar la ecuación de movimiento. Una alternativa es plantear el teorema de la energía en el sistema relativo (en que la reacción es de potencia nula). Las otras dos fuerzas que aparecen son conservativas: la elástica del resorte y la fuerza ficticia de arrastre que es centrífuga. Sus energías potenciales (a menos de constantes) tienen la misma forma pero con signos diferentes. Para la frecuencia angular dada gana la fuerza ficticia centrífuga. Por eso la posición en

$\varphi = 0$ es estable.

Lo que creo que querés hacer es plantear que la ecuación de movimiento a partir de esa ley de conservación te daría:

$m R^2 \ddot{ \varphi } + \frac{ \partial U_{eff}}{\partial \varphi } = 0$

Pero entonces la derivada de la energía potencial efectiva respecto a

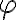$\varphi$ te debería quedar proporcional a sen

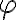$\varphi$ y no - sen

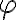$\varphi$ .

Saludos:

Ricardo.