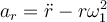Buenas, mi duda en este ejercicio está en como levantar el valor absoluto de la reacción normal de la guia (|N|), al ejercicio lo intenté resolver aplicando la segunda ley de Newton, para ello me tome una base de versores solidaria a la guía, er , e\Theta donde er es radial saliente y e\Theta acompaña la rotación en sentido antihorario, me parece que a priori no sabemos el sentido de la reacción normal de la guía solo sabemos que es según e\Theta, ya que tenemos un vínculo bilateral, proyectando la 2da ley de Newton en e\Theta obtuve que el signo de la reacción normal (N) depende del signo de r punto (siendo r la distancia de la partícula al centro del disco) N=2m.w.rpunto , intenté hallar el signo de r punto en un entorno del instante inicial pero no pude por ese lado ya que en la letra aclara que en el instante inicial la partícula se encuentra en reposo respecto a la guía tambien intente ver en un entorno del instante inicial como varía r pero tampoco fue muy efectivo, entonces procedí a resolver el ejercicio suponiendo que |N|=N y proyectando la 2da ley de Newton en er, quisiera saber si esto es correcto o se puede comprobar que la reacción normal es siempre en un sentido determinado. Saludos
Hola, Carlos. Tu planteo parece bastante coherente y, en realidad, es difícil establecer reglas que se puedan aplicar con gran generalidad. Tu pregunta me hizo pensar un buen rato; eso quiere decir que es una pregunta muy buena.
En este caso, lo que podemos pensar es qué pasa si, por alguna razón, tuvieras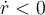 en alguna parte del movimiento. Si esto ocurre, entonces la partícula se está dirigiendo hacia el centro del círculo y la fuerza de fricción sobre la partícula quedaría apuntando en dirección opuesta, centrífuga. Como la fuerza neta en la dirección radial es, justamente, esa fuerza, no estaría apareciendo la fuerza centrípeta necesaria para este movimiento. Por lo tanto, podemos afirmar que
en alguna parte del movimiento. Si esto ocurre, entonces la partícula se está dirigiendo hacia el centro del círculo y la fuerza de fricción sobre la partícula quedaría apuntando en dirección opuesta, centrífuga. Como la fuerza neta en la dirección radial es, justamente, esa fuerza, no estaría apareciendo la fuerza centrípeta necesaria para este movimiento. Por lo tanto, podemos afirmar que 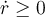 .
.
En este caso, lo que podemos pensar es qué pasa si, por alguna razón, tuvieras
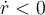 en alguna parte del movimiento. Si esto ocurre, entonces la partícula se está dirigiendo hacia el centro del círculo y la fuerza de fricción sobre la partícula quedaría apuntando en dirección opuesta, centrífuga. Como la fuerza neta en la dirección radial es, justamente, esa fuerza, no estaría apareciendo la fuerza centrípeta necesaria para este movimiento. Por lo tanto, podemos afirmar que
en alguna parte del movimiento. Si esto ocurre, entonces la partícula se está dirigiendo hacia el centro del círculo y la fuerza de fricción sobre la partícula quedaría apuntando en dirección opuesta, centrífuga. Como la fuerza neta en la dirección radial es, justamente, esa fuerza, no estaría apareciendo la fuerza centrípeta necesaria para este movimiento. Por lo tanto, podemos afirmar que 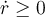 .
.---
En realidad el argumento anterior tiene una sutileza: la componente radial de la aceleración es, en realidad
Cabe preguntarse qué tan seguros podemos estar de que esa expresión va a ser negativa (o cero). La única manera en que 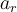 puede ser positiva es si
puede ser positiva es si 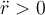 . Pero si en
. Pero si en 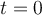 teníamos
teníamos 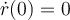 (reposo relativo), entonces no podemos llegar a observar
(reposo relativo), entonces no podemos llegar a observar 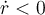 (partícula moviéndose hacia el centro) y a la vez tener
(partícula moviéndose hacia el centro) y a la vez tener 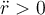 (
(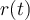 acelera en la dirección positiva, alejándose del centro).
acelera en la dirección positiva, alejándose del centro).
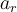 puede ser positiva es si
puede ser positiva es si 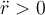 . Pero si en
. Pero si en 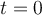 teníamos
teníamos 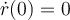 (reposo relativo), entonces no podemos llegar a observar
(reposo relativo), entonces no podemos llegar a observar 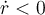 (partícula moviéndose hacia el centro) y a la vez tener
(partícula moviéndose hacia el centro) y a la vez tener 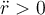 (
(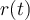 acelera en la dirección positiva, alejándose del centro).
acelera en la dirección positiva, alejándose del centro).Si estuviste pensando cosas por el estilo de lo anterior, enhorabuena por la profundidad del razonamiento. Pero tampoco pienso que sea tan necesario.
---
En definitiva, el método que usaste de suponer 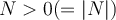 es válido, siempre y cuando estés dispuesto a analizar todas las alternativas.
es válido, siempre y cuando estés dispuesto a analizar todas las alternativas.
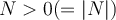 es válido, siempre y cuando estés dispuesto a analizar todas las alternativas.
es válido, siempre y cuando estés dispuesto a analizar todas las alternativas.Espero haber podido ayudar (no sé si es la explicación más simple). Continúa trabajando y contanos cómo te va más tarde.
Saludos,
NC
NC
Perfecto, quedó muy claro y ya pude terminar de resolverlo por el lado de llegar a un absurdo suponiendo que la fuerza de fricción pudiese apuntar en algún momento en el sentido positivo según er. Muchas gracias por la ayuda!