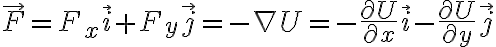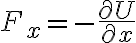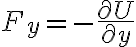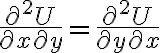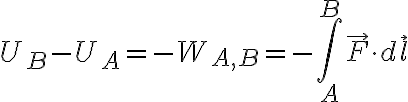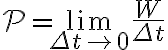una consulta, cómo se concluye que es una fuerza no conservativa y no una fuerza residual, pregunto porque en la parte d habla del potencial y ahí varia, porque si es residual el potencial no es 0 y si no conservativa el potencial si es 0
Estimada:
No entiendo mucho tu pregunta. Una fuerza no conservativa sería lo mismo que una fuerza residual. Por otro lado las fuerzas residuales o no conservativas no tienen definido un potencial.
Por las dudas aclaro: para que una fuerza sea conservativa el trabajo para ir desde un punto A a un punto B tiene que ser independiente de la trayectoria (solo depende de las posiciones inicial A y final B). SI el trabajo depende de la trayectoria entonces la fuerza es no conservativa o lo que es lo mismo, residual. Las fuerzas conservativas además solo deben depender de la posición (no pueden depender de la velocidad ni el tiempo).
Por otro lado están las fuerzas de potencia nula, que no trabajan.
Pero volviendo a las fuerzas conservativas, en ellas el trabajo en una curva cerrada es cero (porque es igual al trabajo de una trayectoria nula). Y las fuerzas cuyos trabajos en curvas cerradas son nulas se pueden obtener a partir de una energía potencial U como:
Acá estoy escribiendo solo en dos coordenadas (como en el ejercicio) para simplificar. Luego:
y
Y además:
Luego si la fuerza es conservativa y existe la energía potencial se debe cumplir que_
Saludos:
Ricardo.
Entiendo tu respuesta, pero ahora me maree un poco porque en el Open fing separa en fuerzas residuales con un potencial no nulo y en fuerzas no conservativas con un potencial nulo
Hola, Valentina. Ten cuidado de no estar confundiendo el concepto de potencial (asociado a la energía potencial de una fuerza, letra usual U) con el concepto de potencia de una fuerza (letra usual P).
La diferencia de potencial de una fuerza conservativa corresponde al trabajo que realiza en una trayectoria entre dos puntos, con el signo opuesto. En cuentas, esto lo escribimos como
La potencia de una fuerza corresponde a la rapidez con que realiza trabajo (qué tan rápido puede causar un cambio de energía). La potencia instantánea se define mediante
Se puede además demostrar que esto último resulta ser el producto escalar entre la fuerza y la velocidad del punto donde se aplica: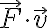 
(¿cómo se demuestra?).
No estaría mal vovler a revisar el video de OpenFing tomando esto en cuenta, a ver qué tal.
Saludos,
NC
Estimada:
Si te confundiste con mi respuesta te sugiero que leas el comienzo de la sección 3.2.3 de los Apuntes de Mecánica Newtoniana del curso 2010 (https://eva.fing.edu.uy/file.php/37/Notas2010/Apuntes_MecNewt.pdf). Allí se clasifican las fuerzas en tres tipos:
1) Fuerzas Conservativas: Su trabajo se puede escribir, a menos de un signo, como la diferencia de una energía potencial en la posición final menos la energía potencial en la posición inicial.
2) Fuerzas de Potencial Nula: No trabajan.
3) El resto de las fuerzas (llamales como quieras), cuyo trabajo puede ser distinto de cero y no se puede escribir como el de las conservativas en función de una energía potencial.
Lo importante es que se puede definir una energía mecánica que es la suma de la energía cinética más todas las energías potenciales. La diferencia de la energía mecánica final menos la energía mecánica inicial es el trabajo de las fuerzas no conservativas.
Si todas las fuerzas son conservativas o de potencia nula, esa energía mecánica se conserva.
Saludos:
Ricardo.