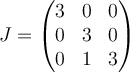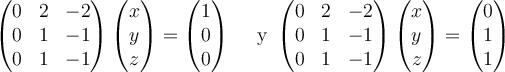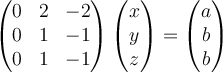Foro de dudas del práctico 4

Hola Melany.

Antes que nada te quería comentar que los sub-bloques de Jordan se ponen en orden creciente por tamaño. O sea, primero el de 1x1 y después el de 2x2.

Así que la forma de Jordan es $J=\left( \begin{matrix} 3 & 0 & 0 \\ 0&3&0\\ 0&1&3 \end{matrix} \right)$

Ahora para hallar la base de Jordan B= {<strong>u, v, w</strong>}

Fijate que si la matriz asociada a T en la base B es J entonces

T(u) = 3u

T(v) = 3v +w => (T-3I) (v) = w

T(w) = 3w

Entonces u y w son vectores propios y v es tal que (T-3I) (v) = w. 

Una forma de hacerlo es teniendo u y w después hallar v resolviendo el sistema 

El tema es que si llamamos v=(x,y,z), no para cualquier w vector propio, el sistema (T-3I) (x,y, z) = w tiene solución.

Fijate que justamente 

$\left( \begin{matrix} 0 & 2 & -2 \\ 0&1&-1\\ 0&1&-1 \end{matrix} \right) \left( \begin{matrix} x\\y\\z \end{matrix} \right)= \left( \begin{matrix} 1 \\ 0 \\ 0 \end{matrix} \right) \quad \text{ y } \left( \begin{matrix} 0 & 2 & -2 \\ 0&1&-1\\ 0&1&-1 \end{matrix} \right) \left( \begin{matrix} x\\y\\z \end{matrix} \right)= \left( \begin{matrix} 0 \\ 1 \\ 1 \end{matrix} \right)$ son sistemas incompatibles.

Entonces tendrías que elegir w  un vector propio, o sea  w=(a, b, b),  de forma tal que el sitema 

$\left( \begin{matrix} 0 & 2 & -2 \\ 0&1&-1\\ 0&1&-1 \end{matrix} \right) \left( \begin{matrix} x\\y\\z \end{matrix} \right)= \left( \begin{matrix} a\\ b \\ b \end{matrix} \right)$

te quede compatible (¿recordás cómo hacías esto en Gal1? Escalerizás y si en la izquierda tenés una fila de ceros, la entrada en la derecha tiene que ser cero; y de ahí sacás la condicón que tiene que cumplir w para que el sistema sea compatible. Lo podés hacer a ojo también je)

Para ese w, cualquier solución del sistema te sirve como  v, y después tenés que tomar u otro vector propio que sea L.I. con w.

Otra forma de hacerlo es hallando primero v.

Fijate que (T-3I)²(v)= (T-3I)(w)=0 (porque w es vep)

Entonces v está en el Ker( (T-3I)²) pero no está en el Ker( (T-3I)) (porque (T-3I) (v) = w≠0)

Entonces v no está en S₃={(x, y, y) } y está en el ker((T-3I)²)

Fijate que si hacés la matriz de T-3I al cuadrado, te da la matriz nula. Entonces ker((T-3I)²)=R³

Entoces v es cualquier vector de R³ que no esté en S₃  (por ejemplo v= (0,0,1)).

Y después haces w= (T-3I) (v) 

y te falta u que es otro vector propio que sea L.I. con w.

Avisame si se entendió

Saludos!

Marianita