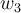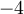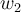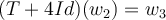Hola,
Cómo están?
Mi duda con este ejercicio surgió a raíz de ver el video que hay colgado de la solución. El profesor utiliza un método o una forma de calcular el vector faltante de la base el cuál yo no venia utilizando.
Usa que el vector w2 de la base de jordan no debe pertenecer al núcleo del subespacio propio asociado a -4 ( valor propio), esto me parece lógico, pero no entiendo porque dice que si debe pertenecer a ker(T+4Id)^2.
¿Porque si debe pertenecer al núcleo de la transformación al cuadrado?
Por otro lado me gustaría confirmar porque no se podría utilizar el método que aparece en las clases de teórico que dada la matriz de Jordan de la transformación:

, obtengo T(w2)= 0.w1-4w2+1.w3 ==> ( T +4Id)(w2)=w3
Espero se entienda,
gracias,
Saludos