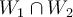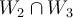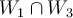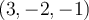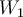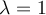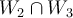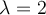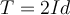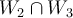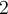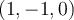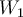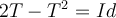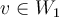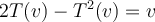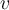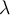Ej 2 parte 5 b)

Ej 2 parte 5 b)

de Nahuel Rossi Permuy -
Número de respuestas: 7

¿Me podrian explicar como hallar los valores propios ? 

Entiendo que por parte 4 del mismo ejercicio, que si W1 es de dim 1 entonces el vector perteneciente es un VEP pero ahora que son dos vectores pertenecientes a W1 ambos son VEP?

Vi temas abajo respuestas a ello pero no me a quedado claro,  desde ya muchas gracias.

En respuesta a Nahuel Rossi Permuy

Re: Ej 2 parte 5 b)

de Gustavo Guerberoff -

Hola Nahuel. Recordá que más arriba se probó que la intersección de subespacios invariantes es también un subespacio invariante. De modo que W_1 \cap W_2 ,   W_2 \cap W_3 y   W_1 \cap W_3 son subespacios invariantes de dimensión 1. Vectores generadores de esos subespacios son (por ejemplo): (3,-2,-1) ,  (1,-1,0)  y  (3,1,1) (respectivamente). Resultan así tres vectores propios de T , y son L.I., de manera que T resulta diagonalizable.

Ahora, para la parte b) hay que aplicar las dos condiciones que se dan. Como base de W_1 se usan los vectores que se obtuvieron en la parte a):  (3,-2,-1) y  (3,1,1) . Esos son vectores propios y en principio podrían corresponder a valores propios diferentes. Pero si se aplica la primera identidad sobre T se obtiene una ecuación cuadrática para los valores propios, cuya única solución es \lambda = 1. La otra identidad es aún más fácil de manipular, aplicándola al vector (1,-1,0) , que es base de W_2 \cap W_3 y es vector propio. Se obtiene así el segundo valor propio \lambda = 2.  
En respuesta a Gustavo Guerberoff

Re: Ej 2 parte 5 b)

de Edgardo Mauricio Tort Schiappacasse -
Hola, no entiendo que significa o como utilizar el dato de 2T-T^2= id
En respuesta a Edgardo Mauricio Tort Schiappacasse

Re: Ej 2 parte 5 b)

de Ana González -
Hola Edgardo,
por la parte anterior sabemos que T tiene tres vectores propios LI por lo tanto existe una base de vectores propios. Ahora el problema consiste en ver cuales son los valores propios.
La segunda condición T=2Id en W_2\cap W_3, nos dice que 2 es el valor propio correspondiente a (1,-1,0). Como los otros dos vectores propios están en W_1, la condición 2T-T^2= Id debe permitir hallarlos.
Tomemos por lo tanto un vector propio v\in W_1, entonces
2T(v)-T^2(v)=v, usando esta condición y que v es vector propio de T asociado a \lambda trata de hallar los posibles valores de \lambda. 
Espero esto te ayude a terminar de resolver el problema.
Saludos
En respuesta a Gustavo Guerberoff

Re: Ej 2 parte 5 b)

de Nicolas Gonzalez Blumberg -
La parte de que los 3 vectores propios son LI es por aquel teorema que dice:

Sean lambda1, lambda2,.., lambdak VAPs dos a dos distintos y v1, v2,...,vk VEPs correspondientes a cada VAP.
Entonces v1, v2,...,vk es LI ??

Por qué puedo asumir que los VAPs asociados a los VEPs que encontré son dos a dos distintos?

Gracias !
En respuesta a Nicolas Gonzalez Blumberg

Re: Ej 2 parte 5 b)

de Mariana Pereira -
No, tal como decís tu, en principio no hay datos sobre los valores propios.
Pero lo que sí obtenés haciendo intersecciones son vectores propios. Y (copiando mensajes anteriores) obtenés que entonces (3,−2,−1), (1,−1,0) y (3,1,1) son vectores propios.

Ahora, esos 3 vectores son LI o LD? Y bueno, hay que plantear una CL de ellos igualada al nulo, y ver si necesariamente los coeficientes de la C.L son cero