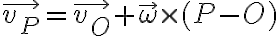Estimado:
En la parte a se pide hallar ambas velocidades respecto a un sistema fijo (el suelo).
En la parte a se pide hallar ambas velocidades respecto a un sistema fijo (el suelo).
En tu solución creo no estás calculando la velocidad de P (solidario a la rueda) respecto a este sistema, Además de que no veo cómo estás considerando el giro de la rueda.
La forma de calcular lo que se pide es la siguiente.
La velocidad del punto de contacto P como perteneciente a la placa es muy fácil ya que es simplemente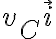 
siendo 
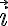el versor hacia la derecha de la solución del compañero Matías. Esto es porque la placa solo se traslada hacia la derecha entonces todos sus puntos tienen la misma velocidad.
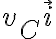siendo 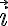el versor hacia la derecha de la solución del compañero Matías. Esto es porque la placa solo se traslada hacia la derecha entonces todos sus puntos tienen la misma velocidad. Para hallar la velocidad del punto de contacto P solidario a la rueda lo más fácil es considerar un sistema de coordenadas fijo en la rueda y hallar la velocidad de arrastre o transporte del punto P en este sistema (que sería la velocidad absoluta de un punto fijo en ese sistema de coordenadas, o sea, solidario a la rueda). Esta estará dada por:
donde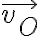 
es la velocidad absoluta (respecto al suelo) del centro del disco (considerado el origen de coordenadas de ese sistema). En la solución del compañero él consideró que 
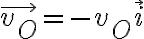, porque orientó la velocidad del centro del disco hacia la izquierda (si ese punto se mueve hacia la derecha este 
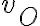será negativo). Luego 
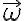es la velocidad angular de este sistema, es decir la velocidad angular de la rueda, y vale 
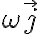, siendo 
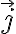un versor perpendicular a la rueda saliente del plano del dibujo (cómo el que dibujó el compañero Matías), con 
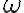la velocidad angular de la rueda en sentido antihorario vista desde el extremo de ese versor, es decir 0.5 rad/s. 
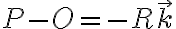, siendo 
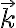un versor hacia arriba (ver figura del compañero Matías). Haciendo esta cuenta (teniendo en cuenta que la base 
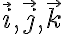que dibujó el compañero Matías no es directa) el resultado es el del miembro derecho de la primer ecuación de mi mensaje anterior (según ).
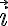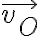es la velocidad absoluta (respecto al suelo) del centro del disco (considerado el origen de coordenadas de ese sistema). En la solución del compañero él consideró que 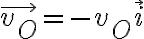, porque orientó la velocidad del centro del disco hacia la izquierda (si ese punto se mueve hacia la derecha este 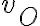será negativo). Luego 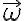es la velocidad angular de este sistema, es decir la velocidad angular de la rueda, y vale 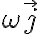, siendo 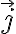un versor perpendicular a la rueda saliente del plano del dibujo (cómo el que dibujó el compañero Matías), con 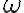la velocidad angular de la rueda en sentido antihorario vista desde el extremo de ese versor, es decir 0.5 rad/s. 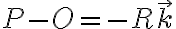, siendo 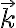un versor hacia arriba (ver figura del compañero Matías). Haciendo esta cuenta (teniendo en cuenta que la base 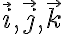que dibujó el compañero Matías no es directa) el resultado es el del miembro derecho de la primer ecuación de mi mensaje anterior (según 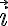). Saludos:
Ricardo.