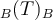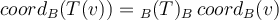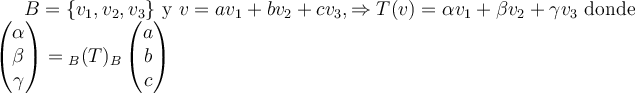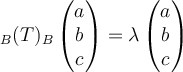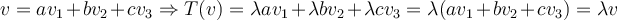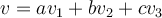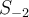3.b

3.b

de Nataly Melanie Ruber Maimo -
Número de respuestas: 2

hola, quiero ver si entendí bien el 3.b, una ve que tengo los valores propios y los subespacios de A, puesto que el polinomio característico, entonces tienen los mismos valores propios, pues bTb es la matriz asociada a T y es A. Entonces uso los mismos valores, y por usar los mismos valores me da el mimso resultado si hago Ker(T-lamdaId), ésto es porque T=A? entonces eso me da el mimso resultado que antes con A, pero ahora viene lo que me marea un toque, tengo que agarrar dos (x,y,z) y sacar las coordenadas de allí usando el viejo resultado pero con los vectores de B, por ejemplo

(x,y,z)=1(1,0,0)-1(1,1,0)+0(1,1,1) y eso da (0,-1,0)

eso con S1 y S2, pero no capto bien por qué, o sea supongo que A y T no son iguales, pero me da el mismo resultado en el ker de antes, por qué no puedo quedarme con el resultado de A y listo? Supongo que es porque al resultado de A lo tengo que "llevar" a T y por eso se hace eso, pero me confunde un toque 

graciass

En respuesta a Nataly Melanie Ruber Maimo

Re: 3.b

de Mariana Pereira -

Hola,
La matriz asociada {}_B(T)_B te dice cómo cambian las coordenadas de un vector (en la base B) cuando le aplicás T, porque usando el Teorema 10 de libro rojo nos queda que
coord_B(T(v))={}_B(T)_B\, coord_B(v)

Esto quiere decir que si 
B=\{v_1, v_2, v_3\} \text{ y } v=av_1+bv_2+cv_3, \Rightarrow T(v)=\alpha v_1+ \beta v_2 + \gamma v_3 \text{ donde } \\ \left( \begin{matrix}\alpha\\ \beta \\ \gamma\end{matrix}\right)= {}_B(T)_B\left( \begin{matrix}a\\ b\\c\end{matrix}\right)

Ahora, si (a,b,c) es vector propio de la matriz asociada, es decir 
{}_B(T)_B\left( \begin{matrix}a\\ b\\ c\end{matrix}\right) = \lambda\left( \begin{matrix}a\\b\\c\end{matrix}\right)
en  lo anterior te quda que   (\alpha, \beta, \gamma)= (\lambda a, \lambda b, \labda c)
y por lo tanto si 
v=av_1+bv_2+cv_3 \Rightarrow T(v)=\lambda a v_1+ \lambda b v_2 + \lambda c v_3= \lambda (av_1+bv_2+cv_3)= \lambda v

O sea si (a,b,c) es vector propio de la matriz asociada con valor propio λ, entonces  v=av_1+bv_2+cv_3 es vector propio de T  también con valor propio λ

(lo anterior es en realidad un sí y solo si y es la Proposición 37 para n=3) .

En este ejercicio como (1,-1,0) es vector propiode A con vap -2 entonces

v=1(1,0,0)-1(1,1,0)+0(1,1,1) =(0,-1,0) es vector propio deT con vap -2.

Saludos
Mariana

PD: OJO que el subíndice de la S es el valor propio λ, en este caso sería S_{-2}