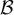No me doy cuenta como sacar el ejercicio 13 si me dan una mano les agradezco
yo hice esto pero no me terminó quedando la parte 2 (la parte 1 creo que si)
pero me quedó la duda de por qué la segunda parte no me queda :/
Hola Aixa y Nataly,
Nataly, en la primera parte empezaste bien, pero al final pusiste que la base B' tiene al vector nulo, lo cual es imposible porque no sería L.I. Además tu manera de escribir las bases como una matriz es confusa, pues hay una en la que los vectores están colgados en fila y en la otra en columnas. Las bases se deben escribir como conjuntos y respetando el orden de los vectores.
Dicho esto, si ya tienes que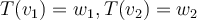
basta con fijar una base B tal que el último vector (
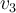) esté en el núcleo y luego ya tienes dos vectores de B' que son justamente las imágenes de los primeros dos vectores de B. Completás el tercero y ya está. Para la segunda parte, las matrices E y F son matrices de cambio de coordenadas.
Nataly, en la primera parte empezaste bien, pero al final pusiste que la base B' tiene al vector nulo, lo cual es imposible porque no sería L.I. Además tu manera de escribir las bases como una matriz es confusa, pues hay una en la que los vectores están colgados en fila y en la otra en columnas. Las bases se deben escribir como conjuntos y respetando el orden de los vectores.
Dicho esto, si ya tienes que
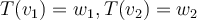basta con fijar una base B tal que el último vector () esté en el núcleo y luego ya tienes dos vectores de B' que son justamente las imágenes de los primeros dos vectores de B. Completás el tercero y ya está. Para la segunda parte, las matrices E y F son matrices de cambio de coordenadas.Espero les sirva esta explicación.
Saludos!
pero si hago T(1,4,5) me da 0 no? porque yo sustituyo en la ecuación de T(x,y,z) y me da (0,0,0)
Sí, pero una transf. lineal no necesariamente transforma una base del dominio en una base del codominio. Este es un caso en el que los dos primeros vectores de B se transforman en dos vectores L.I. pero el tercero no, por tanto tienes que completar esos dos con otro de manera que obtengas una base del codominio.
podrias ver si esto e correcto? Estoy estudiando un poco sola porque trabajo y voy llevando el curso de a poco
me di cuenta que esta mal los vectores v1 y v2
Ahora si EL Otro esata todo mal ni lo mires me da verguenza. Agradeceria si lo miras gracias
Hola, Elena:
Está correcto.
Saludos,
Marco
Está correcto.
Saludos,
Marco
Hola! acá pude resolverlo casi todo pero me queda la duda si w3 puede ser cualquier vector ya que T(V1)=0*W3 ? o porque es (0,0,1)
Es porque multiplicando B'(T)B *(X,Y,Z) y me queda queda un vector de la forma (0,0,1)Z ? y al ser B' la base de llegada entonces este vector que tiene dimensión 1 es una base de B'?
Hola, Juan:
El tercer vector de
está en el núcleo de 
. Habiendo elegido ya los primeros dos vectores de y 
, sí, puedes tomar el tercer vector de como cualquier vector, siempre y cuando forme un conjunto linealmente independiente con los primeros dos vectores de .
Saludos,
Marco
El tercer vector de
está en el núcleo de . Habiendo elegido ya los primeros dos vectores de y , sí, puedes tomar el tercer vector de como cualquier vector, siempre y cuando forme un conjunto linealmente independiente con los primeros dos vectores de .Saludos,
Marco