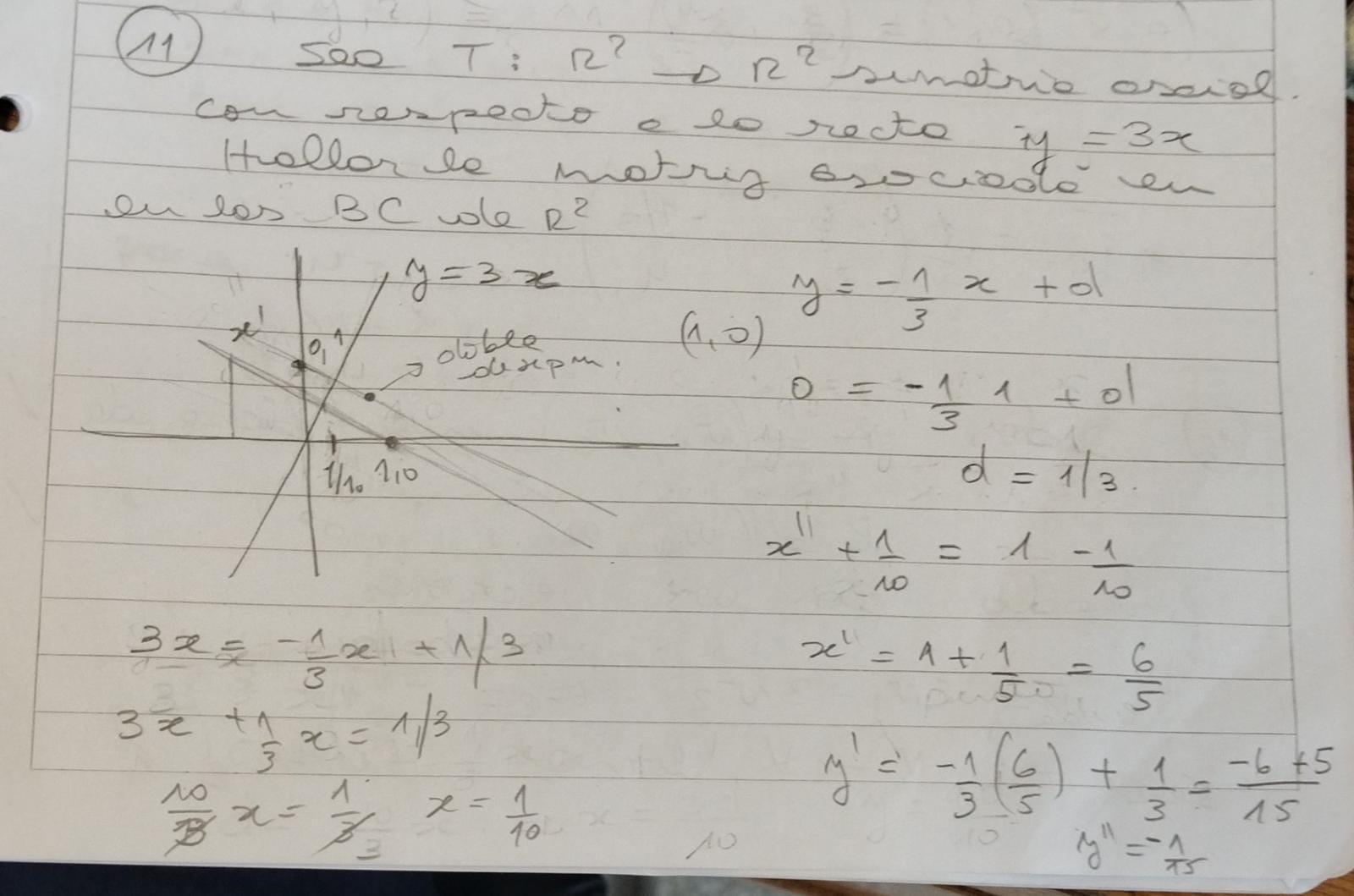
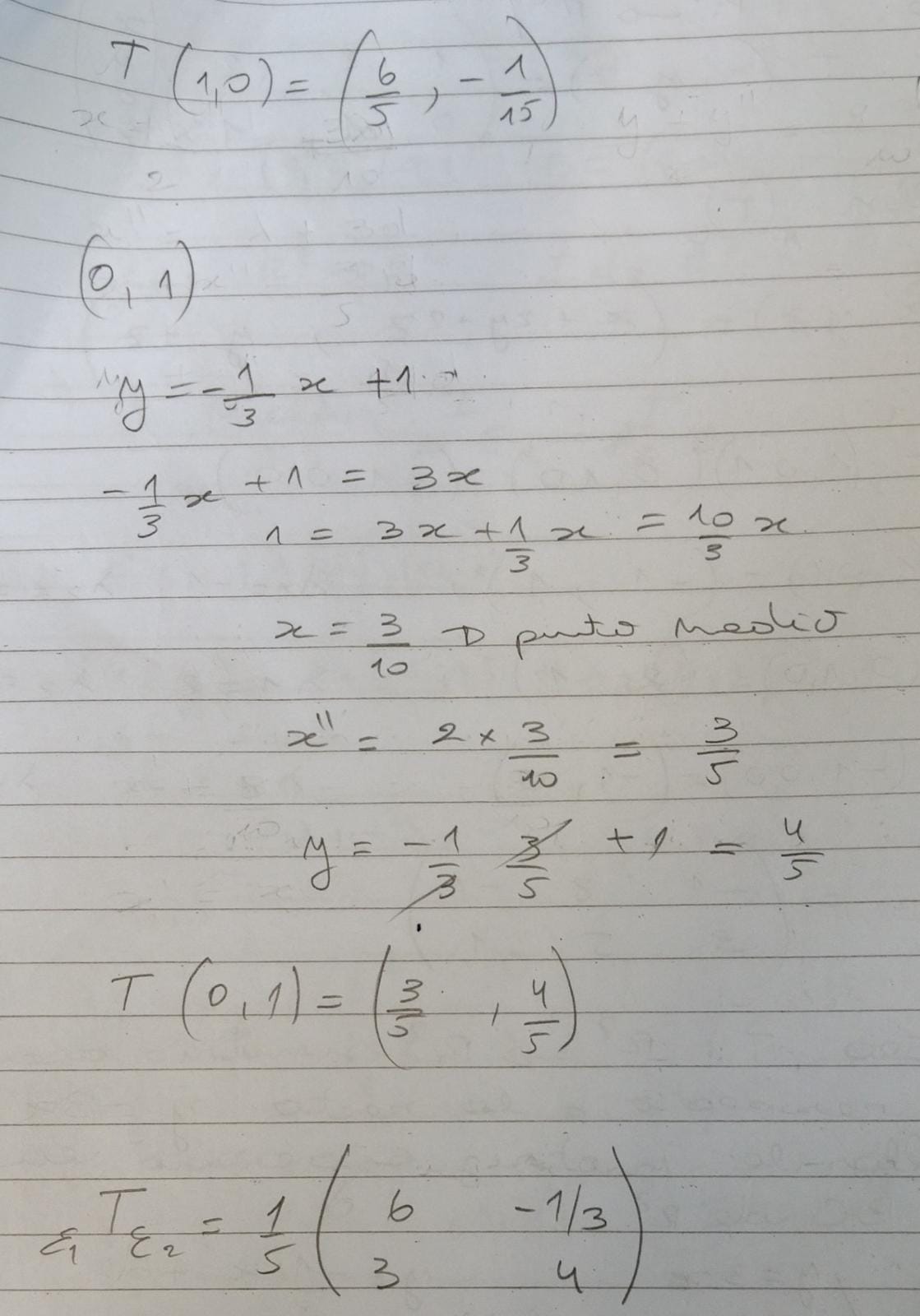Buena, me gustaría pedirles algún pique para para poder atacar el ejercicio, ya que de momento no veo como empezarlo.
Saludos
Francisco.
Buena, me gustaría pedirles algún pique para para poder atacar el ejercicio, ya que de momento no veo como empezarlo.
Saludos
Francisco.
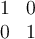 no estoy seguro que es lo que estoy haciendo mal.
no estoy seguro que es lo que estoy haciendo mal.

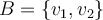 , es decir elegir vectores
, es decir elegir vectores 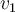 y
y 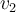 que cumplan las condiciónes que escribiste. Porejemplo
que cumplan las condiciónes que escribiste. Porejemplo 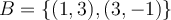 , donde elegí arbitrariamente un vector que pertenece a
, donde elegí arbitrariamente un vector que pertenece a 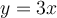 y otro que sea perpendicular a esa recta.
y otro que sea perpendicular a esa recta.hola pede ser que este procedimiento este bien?? gracias