Juan,
A partir de las expresiones de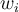 en función de
en función de 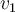 y
y 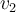 , tienes las coordenadas de los vectores de la base
, tienes las coordenadas de los vectores de la base 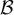 en la base
en la base 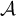 , por lo que puedes calcular la matriz de cambio de base de
, por lo que puedes calcular la matriz de cambio de base de 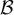 a
a 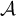 . Tomando la inversa de esta última, tienes la matriz de cambio de
. Tomando la inversa de esta última, tienes la matriz de cambio de 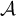 a
a 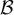 . Con esto es suficiente para hallar
. Con esto es suficiente para hallar  , ya que
, ya que  .
.
Y no, no es cierto que . Si te fijas en la matriz
. Si te fijas en la matriz  , la primera columna te dice las coordenadas de
, la primera columna te dice las coordenadas de  en la base
en la base  . Al ser 1 y 0 estas coordenadas, tienes que
. Al ser 1 y 0 estas coordenadas, tienes que  .
.
Saludos,
Marco
A partir de las expresiones de
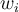 en función de
en función de 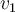 y
y 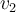 , tienes las coordenadas de los vectores de la base
, tienes las coordenadas de los vectores de la base 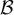 en la base
en la base 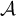 , por lo que puedes calcular la matriz de cambio de base de
, por lo que puedes calcular la matriz de cambio de base de 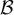 a
a 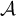 . Tomando la inversa de esta última, tienes la matriz de cambio de
. Tomando la inversa de esta última, tienes la matriz de cambio de 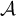 a
a 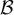 . Con esto es suficiente para hallar
. Con esto es suficiente para hallar  , ya que
, ya que  .
.Y no, no es cierto que
 . Si te fijas en la matriz
. Si te fijas en la matriz  , la primera columna te dice las coordenadas de
, la primera columna te dice las coordenadas de  en la base
en la base  . Al ser 1 y 0 estas coordenadas, tienes que
. Al ser 1 y 0 estas coordenadas, tienes que  .
. Saludos,
Marco