Buenas, me gustaria saber como puedo hallar la expresion de la transformacion lineal.
Gracias.
Buenas, me gustaria saber como puedo hallar la expresion de la transformacion lineal.
Gracias.
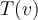 en la base correspondiente para cualquier vector
en la base correspondiente para cualquier vector 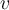 del dominio de la transformación
del dominio de la transformación  . Espero esta información te ayude a resolver el problema.
. Espero esta información te ayude a resolver el problema. . Recuerda que puedes hallar las coordenadas de
. Recuerda que puedes hallar las coordenadas de  en la base de
en la base de 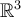 hallando las coordenadas de
hallando las coordenadas de  en la base de
en la base de 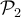 y aplicando la igualdad
y aplicando la igualdad  . Una vez que tengas
. Una vez que tengas  , digamos que da
, digamos que da 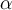 ,
, 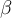 y
y 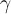 , puedes calcular explícitamente
, puedes calcular explícitamente  (te sugiero que recuerdes qué significa que
(te sugiero que recuerdes qué significa que 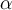 ,
, 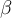 y
y 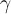 sean las coordenadas de
sean las coordenadas de  en la base
en la base 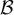 ).
).