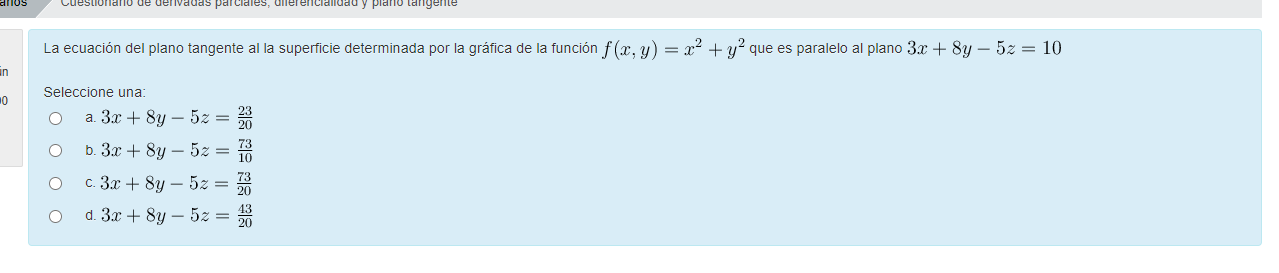
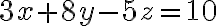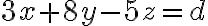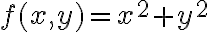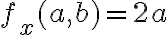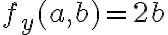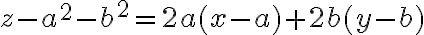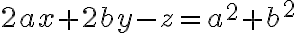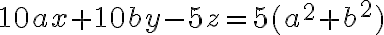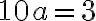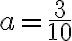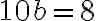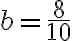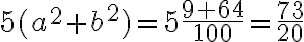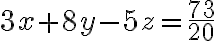Buenas, me contré en el cuestionario con cálculos de plano tangente.
Lo que intenté fue hallar el gradiente, con eso tengo los vectores que generan el plano tangente en cada punto del paraboloide.
Lo que intente luego fue igualar las derivadas (gradiente) con las derivadas del plano pero no llegue a nada.
Me pueden dar una mano a como resolverlo?