Hola! Me parece que me estoy mareando un poco con el tema de los cilindros cuando estan desplazados hacia algun sentido. No me queda claro como corresponderia integrar. Primero se me ocurrio hacer un cambio de variable de forma que ahora considero como si estuviera integrando desde el centro del cilindro, este cambio de variable seria u= x+1 y creo que eso me resultaria facilitando las polares quizas? de todas formas no me queda claro, me podrian dar alguna ayuda? gracias!
Hola,
Primero como estamos en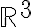 
me gusta más el nombre cilíndricas en vez de polares.
Como correspondería integrar depende mucho del problema, no hay una receta. En general las cosas que uno intenta es hacer lo que hiciste vos o hacer cilíndricas sin mover el cilindro al origen. Si eso no funciona entonces uno tendría que ingeniárselas, estudiar al problema en particular, siempre pensando que los cambios de variables involucran modificar el dominio pero también la función, y hay que hacer que los dos queden manejables.
Lo que vos propones de primero hacer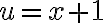 
, que correspondería al cambio de variable 
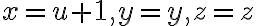(en 
y en 
no hago nada) traslada el cilindro, pero no al origen ojo. La ecuación del cilindro es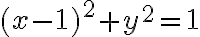 
y vos queres que quede 
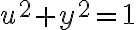, entonces 
.
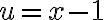Entonces, las dos opciones clásicas digamos serían
Lo que vos propones,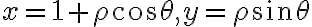 
y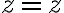 
(Hice los dos cambios de variable de una, traslade el cilindro y pose cilíndricas, todo en una)
Solamente cilíndricas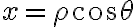 
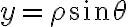y 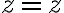(que es lo que propone la letra del problema)
Cualquiera de las dos estrategias funciona en este ejemplo.
Espero haber arrojado un poco de luz al asunto. No se si respondí tu pregunta, sino seguimos discutiendo
Saludos