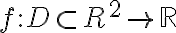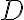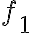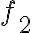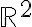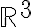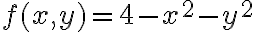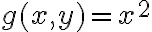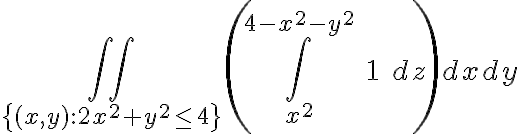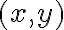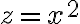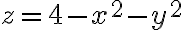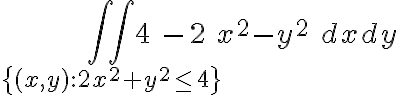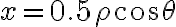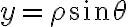CDIVV-2S: Duda ejercicio 7.D

Buenas, para plantear este ejercicio intenté resolverlo como si fuera calcular el volumen de una integral triple, y utilizando el cambio de variable de cilíndricas, pero estoy un poco perdido y no se como continuar.

Llegué a estas condiciones z=r^2.(cos(theta))^2, 4-r^2=z, pero al momento de hacer la integral triple, no supe como hallar los intervalos de cada integral.

Me fije en el canal de youtube y vi que hicieron este ejercicio en la clase "Clase pr 10 - 2", no logro comprender del todo lo que se plantea para resolverlo, el profe dice de hacer la integral doble de las funciones encerradas, pero no entiendo por que es doble y no triple. Mi suposición es que tengo z=4-x^2-y^2, entonces para cada x e y, queda asignado un z, por lo que, en realidad z esta en función de x e y. Entonces en realidad tengo dos variables, x e y, no? z queda dado por ellos.

Lo mismo ocurre con z=x^2, no?

Si es así, entonces no entiendo que es lo que se calcula cuando hacemos una integral triple, porque en este caso, calculamos el volumen a partir de una integral doble.

Pero si hacemos el calculo de una integral triple, no debería de ser el mismo concepto que para una integral doble.

Gracias, saludos!

Re: Duda ejercicio 7.D

de Alejandro Bellati - viernes, 27 de noviembre de 2020, 20:05

Hola,

El tema de utilizar cilíndricas así es que el dominio no queda lindo escrito en termino de estas nuevas variables.

Respecto al concepto de integrales triples y dobles.

En cálculo 1 la integral de una función de una variable da el valor del área que se encuentra "debajo" de la gráfica de la función.
En cálculo 2 tenemos más integrales. Si tenemos $f:D \subset R^2 \to \mathbb{R}$ entonces la integral doble de dicha función da el volumen debajo de la gráfica, sobre el dominio $D$ . Entonces esto es una forma de calcular volúmenes. Al igual que en calculo 1, si se tiene dos funciones $f_1$ y $f_2$ , la integral doble de la resta de estas funciones da el volumen entre las gráficas (con el signo correcto).
Ahora también en calculo 2 tenemos otras formas de calcular áreas y volúmenes. Dado un conjunto $D$ en $\mathbb{R}^2$ entonces la integral doble de la función f(x,y) = 1 para todo x,y, sobre el dominio D es igual al área de dicho conjunto.
De la misma forma si tenemos un conjunto $D$ en $\mathbb{R}^3$ entonces la integral triple de la función f(x,y,z) = 1 para todo x,y,z sobre el dominio D es igual al volumen de dicho conjuntos

Volviendo al ejercicio, en el mismo se pide calcular un volumen. Para esto podemos aplicar en general el punto 4), y a veces el punto 2). Digo a veces el punto 2) porque para aplicar el método 2 necesitamos que el conjunto al cual queremos calcular el volumen se corresponda con el volumen por debajo de la gráfica de una función de dos variables, o comprendida entre la grafica de dos funciones de dos variables. En este caso podemos ver que al conjunto al cual queremos calcular el volumen lo podemos expresar como los puntos del espacio que se encuentran por debajo de la función $f(x,y) = 4 -x^2 -y^2$ y por encima de $g(x,y) = x^2$ . Por eso integramos la resta de las funciones. Alternativamente podíamos haber hecho el enfoque de la integral triple, que quedaría así

$\underset{\{(x,y): 2x^2 +y^2 \leq 4\}}{\iint}\left( \int_{x^2}^{4-x^2-y^2}\ 1\ dz\right) dxdy$ (ya hice parte del Fubini)

ya que las variables $(x,y)$ se mueven en esa elipse (como vimos en clase) ,y para cada $(x,y)$ en esa elipse la variable $z$ se mueve entre $z = x^2$ y $z = 4-x^2-y^2$ . Si realizas la primera integral queda

$\underset{\{(x,y):2x^2 +y^2 \leq 4\}}{\iint} 4-2x^2-y^2\ dxdy$

que es justamente la integral doble de la resta de las funciones!! lo cual muestra que los dos métodos coinciden.

Para seguir resolviendo la integral habría que hacer un cambio de coordenadas a polares adaptadas a una elipse... o sea que no funciona bien simplemente polares. Pero si haces $x = 0.5 \rho \cos \theta$ $y = \rho \sin \theta$ entonces vas a poder escribir el dominio bien e integrar sin problemas (intentalo).

La idea es esa. Coméntame si respondí tu pregunta, sino iteramos!

Saludos