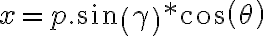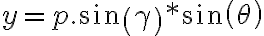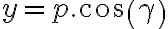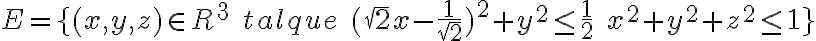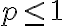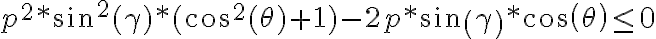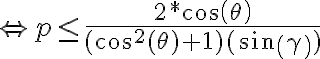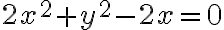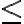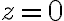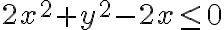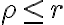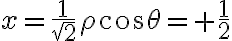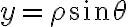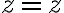Foro Práctico 10

Buenas noches, 

Estoy con este ejercicio, pero estoy trancado y no se como puedo seguirlo. 

Tengo una esfera de radio 1 y centro 0. Y un cilindro medio ovalado de ecuación 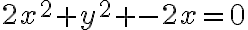$2x^2 + y^ 2 + -2x = 0$. 

Generalmente en estos casos que tengo una esfera, tengo entendió que lo mejor es hacer un cambio de variable esférico. 

Quedando algo así: 

$x = p.sin( \gamma)*cos( \theta)$

$y = p.sin( \gamma)*sin( \theta)$

$y = p.cos( \gamma)$

Primero por la forma del dominio a integrar tenemos que es simétrico. Por lo tanto la voy a dividir por 4. Y solo trabajar en el siguiente dominio: 

$E = \lbrace{ (x,y,z) \in R^3 \quad tal que \quad (\sqrt{2}x - \frac{1}{\sqrt{2}})^2 + y^2 \leq \frac{1}{2} \quad x^2 +y^2+z^2 \leq 1 }\rbrace$

La 2º inecuacion nos dice que $p \leq 1$

Usando la 1º ecuacio despejando p con la intención de buscar una cota superior nos queda: 

 $p^2*sin^2( \gamma )*(cos^2( \theta ) +1 )-2p*sin( \gamma)*cos( \theta) \leq 0$

$\Leftrightarrow p \leq \frac{2*cos( \theta) }{(cos^2( \theta ) +1 )(sin( \gamma ))}$

Es lógico que esta ecuación no nos dice nada si no forzamos a que la misma al menos sea menor o igual que 1, ya que esta es una cota superior de 'p' mas chica que tenemos: 

Osea: 

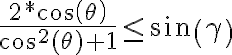$\frac{2*cos( \theta) }{cos^2( \theta)+1 } \leq sin( \gamma)$.  Es importante esta inecuacion, ya que hay casos donde la misma no se cumple restringiendonos solamente cuadrante positivo (x,y,z). Por ejemplo probar con tita = pi/6 y fi = pi/4. 

Probé hacer baskaras y me quedo que 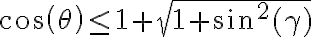$cos( \theta) \leq 1 + \sqrt{1+sin^2( \gamma) }$ Pero el hecho de tener esa raiz cuadrada y un arcos me hace sospechar que eso no va por ahi

El problema es que aquí, una cosa que para nosotros es trivial es que gama se puede mover desde 0 hasta pi/2. Ta que el cilindro literalmente legado a el. El tema es ¿Como puedo generar una mejor acotación para tita? ¿Esa acotación para 'r' es la mejor que puedo conseguir? 

Les pido ayuda con eso, no me esta saliendo con esféricas. 

Saludos

Daniel