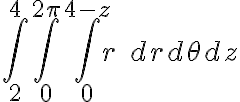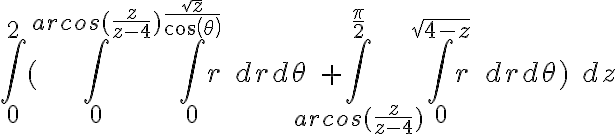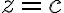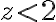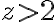Ejercicio 7d | Problema con el cambio de variable con z < 2

Ejercicio 7d | Problema con el cambio de variable con z < 2

de Daniel Padron Simon -
Número de respuestas: 2

Buenas noches, 

Estuve trabajado con este ejercicio sin tener éxito. 

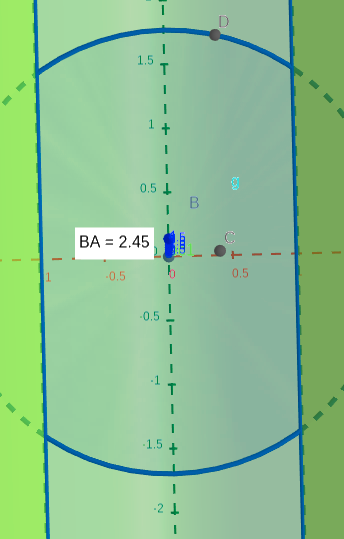
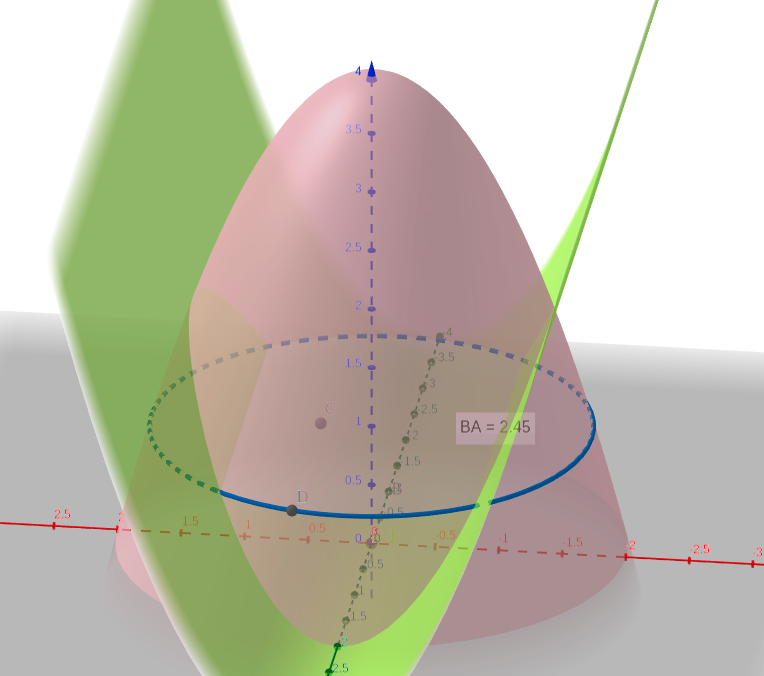
Adjunto algunas fotos para apoyar el razonamiento futuro para que me ayuden con el. La Imagen 2º es la del dominio en general, mientras que un conjunto de nivel en un z menor a 2. 


Por simplificar el ejercicio decidimos separar z en dos intervalos, el mayor a 2 y el menos a 2. 

El primero de ellos es relativamente sencillo. 

Nos queda  \int_{2}^{4} \int_{0}^{2\pi} \int_{0}^{4-z}{r} \quad dr d \theta dz

El problema llega con la segunda, ya que al fijar un z, tenemos que podes calcular el área de la 1º imagen (mirar adjunto). 

Lo mas intuitivo aprovechando la forma de dominio seria dividir el área en 4 y solo calcular una de ellas por simétrica. 

Lo cual nos quedaría que 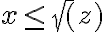 x \leq \sqrt(z)  Usando la primera de las ecuaciones de la letra. 

AL fijar también un x dentro de ese rango nos queda que 0 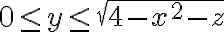 0 \leq y \leq \sqrt{4-x^2-z}

Quedando la integral: 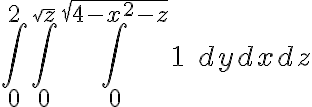 \int_{0}^{2} \int_{0}^{\sqrt{z}} \int_{0}^{\sqrt{4-x^2-z}}{1} \quad dy dx dz . El problema con esa ecuación es que queda espantosa a la hora de operar con ella. Igualmente por calculadoras de integrales se que la superficie es la misma que segun las respuestas del semestre pasado: https://www.wolframalpha.com/input/?i=2pi+%2B+%E2%88%AB%E2%88%AB%E2%88%AB+4+dy+dx+dz+0+to+2+%2C+0+to+sqrt%28z%29+%2C+0+to+sqrt%284-x%5E2-z%29 

Por lo que decidí intentar hacer cilíndricas. Con lo cual no llegue a absolutamente nada útil, solamente a una integral pero que la anterior. Ya que esta es de la forma: 

\int_{0}^{2} ( \int_{0}^{arcos( \frac{z}{z-4}) } \int_{0}^{ \frac{\sqrt{z}}{cos( \theta) } }{r} \quad dr d \theta \quad + \int_{arcos( \frac{z}{z-4}) }^{ \frac{\pi}{2} } \int_{0}^{\sqrt{4-z}}{r} \quad dr d \theta ) \quad dz . 


Por lo cual, les voy a pedir ayuda en dos cosas. 

1) Me pueden dar una mano en como encontrar la integral con ciclindricas, no me estoy dando cuenta. 

2) Como podemos integrar de forma prodente sin ver el dominio en forma de dibujo? Sobre todo pregunto pensando en la ausencia de geogebera y derivados en periodos de evaluacion


Saludos y gracias

Daniel 
Adjunto Captura de pantalla de 2020-11-24 02-43-14.png
Adjunto Captura de pantalla de 2020-11-24 02-43-55.png
En respuesta a Daniel Padron Simon

Re: Ejercicio 7d | Problema con el cambio de variable con z < 2

de Daniel Padron Simon -

Buenas, 


Ya pude solucionar el problema. 


Lo que hice fue tomar la intersepcion donde la "copa" que la funcion x^2. 

Ahi tomas la funcion de la copa menos la de la parábola en ese dominio y queda simple a partir de ahi. 

En respuesta a Daniel Padron Simon

Re: Ejercicio 7d | Problema con el cambio de variable con z < 2

de Veronica Rumbo -

Hola Daniel. No entendí bien qué hiciste al final. Igual quiero hacer un comentario respecto a tu mensaje original, en especial respecto a la pregunta

"Como podemos integrar de forma prodente sin ver el dominio en forma de dibujo? Sobre todo pregunto pensando en la ausencia de geogebera y derivados en periodos de evaluacion"

Mi primer respuesta a eso es que en este tipo de ejercicios es muy importante lograr algo parecido a una visualización del conjunto. Y especialmente en una etapa inicial ayudarse de herramientas como geogebra me parece una excelente idea. Las figuras que pusiste en el mensaje son muy oportunas.

Entiendo, sin embargo, la preocupación: ¿Qué hago en un parcial, donde tengo sólo hojas y un lápiz? Graficar esos conjuntos tridimensionales es a veces difícil pero tenés los conjuntos de nivel. la figura que pusiste "vista de arriba" podés obtenerla así y ese estudio te permite hacerte una idea gráfica del conjunto "por rebanadas" digamos.

En el caso del ejercicio si tomás los subconjuntos de la forma z = c se desprenden tres casos distintos que están en la imágen que adjunto y que te dan la pista de que es conveniente separar las regiones z< 2 y z >2. También te ayudan, en cada uno de esos casos, a definir bien las regiones de integración en las dos variables restantes.

Saludos