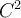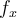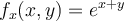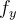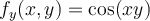ejercicio 8

ejercicio 8

de Matias Carricart Ponce -
Número de respuestas: 1

Hola, no entiendo porque no existe una función que cumpla con estas características ya que usando la definición que dice que una función es de clase Cn, con n ≥ 1, si existen todas sus derivadas parciales de orden n y son continuas, entonces si debería existir una función ya que las derivadas parciales segundas existen y son continuas. 

sin embargo es cierto también que las derivadas parciales segundas no cumplen con la propiedad que deben ser iguales (propiedad solo valida para C2 ) entonces no se como pensarlo ya que la definición y la propiedad usada en la resolución del practico son contradictorias.

muchas gracias.


 



En respuesta a Matias Carricart Ponce

Re: ejercicio 8

de Veronica Rumbo -

Hola Matías. Fijate que lo que te pide el ejercicio es encontrar (si fuera posible) una función f que cumpla a la vez las condiciones:

  • Ser de clase C^2
  • Su derivada parcial f_x es f_x(x,y) = e^{x+y}
  • Su derivada parcial f_y es f_y(x,y) = \cos(xy)
Es verdad que si existiese una función que verifique los dos últimos ítems, sus derivadas parciales de orden 2 serían contínuas (y lo podés constatar derivando las derivadas parciales primeras dadas). Pero siempre estamos poniendo la hipótesis de "si existiese". Y no sabemos si existe. De hecho eso es lo que queremos determinar.

Por esa razón, el efoque adecuado es el que sugerís después (y no hay contradicción ninguna entre eso y la definición). No pueden suceder los tres ítems que puse arriba simultáneamente, ya que toda función f de clase C^2 debe tener derivadas segundas cruzadas iguales, lo cual no ocurre en este ejemplo.