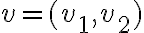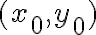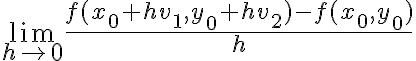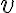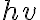existencia de derivadas direccionales.

existencia de derivadas direccionales.

de Facundo Campal Caputti -
Número de respuestas: 5
Hola, no me queda claro cual es la condición que se tiene que cumplir para afirmar la existencia de las derivadas direccionales.

Saludos.

En respuesta a Facundo Campal Caputti

Re: existencia de derivadas direccionales.

de Federico Carrasco Ferretti -

Para que exista la derivada direccional en la dirección v=(v_1,v_2) en el punto (x_0,y_0) necesitas que exista el límite

\displaystyle\lim_{h\to 0}\frac{f(x_0+hv_1,y_0+hv_2)-f(x_0,y_0)}{h}. En caso de existir ese es el valor de la derivada direccional de f en la dirección v en el punto (x_0,y_0).

Si lo que queres es que existan todas, necesitas que para cualquier v exista ese límite.
En respuesta a Federico Carrasco Ferretti

Re: existencia de derivadas direccionales.

de Diego Ismael Marichal Chavez -

hola, tengo una duda respecto a el ejercicio 5, este tiene que ver con esto, pide probar que existen todas las derivadas direccionales en (0,0), pero como es una funcion a trozos no me queda claro, a lo que llegue es qeu me queda el limite de f(hv1,hv2)/ h cuando h teinde a 0, pero como es en trozos no se que elegir. No se si me explico.

Saludos y mcuhas gracias

Diego : D

En respuesta a Diego Ismael Marichal Chavez

Re: existencia de derivadas direccionales.

de Veronica Rumbo -

Eso va a depender del vector dirección v que consideres.

Mi consejo es que grafiques el dominio con las regiones correspondientes, y luego vayas viendo para los distintos v posibles, en que región cae el vectorcito hv donde la idea es que h es cercano a cero.