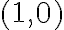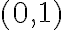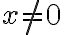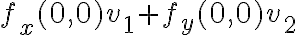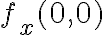Buenas, en este ejercicio nos pide hallar la diferenciabilidad en ciertos puntos. Con la condición suficiente de diferenciabilidad, sabemos que f es diferenciable en un pto si las derivadas parciales existen en una bola con centro en ese punto y ademas ambas derivadas parciales son continuas en ese punto.
En este ejercicio, las derivadas parciales quedan:
∂f/∂x(x, y) = 2x sen(1/x) − ((x^2 + y^2 )cos(1/x))/x^2 + ye^xy
∂f/∂y(x, y) = 2y sen(1/x) + xe^xy.
∂f/∂v(0,y)=0
Por lo tanto en cualquier punto que tenga x=0 o x ->0 las derivadas parciales no serían continuas en ese punto o se irían a infinito.
Mi duda va a que en la solución de este ejercicio en el práctico del semestre pasado dice lo siguiente: Como las derivadas parciales son continuas en la región x /= 0, necesariamente f es diferenciable en esta región. Y termina diciendo que f es diferenciable en el punto (0,0). Pero ∂f/∂v(0,y)=0 y ∂f/∂x(0,0) = 2x sen(1/x) − ((x^2 + y^2 )cos(1/x))/x^2 + ye^xy = ((x^2 + y^2 )cos(1/x))/x^2=acotado*(x^2 + y^2 )/x^2. Y haciendo polares queda: 1/cos(tita)^2. Por lo tanto depende de tita, entonces no se cumple que sea igual a 0. Por lo tanto la derivada no me queda continua en (0,0) -> f no seria diferenciable en (0,0).
Me gustaría saber si la solución del semestre pasado esta mal o si tengo algún error de concepto. Muchas gracias