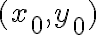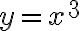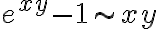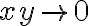Hola, haciendo estos ejercicios me surgió una duda en cuanto a determinar la continuidad.
Para todos estos ejercicios seguí la misma idea, en particular para el 4.c) lo que hice fue tomar limy→0 f(x0,y) y ver que pare que sea continua el lim tiene que ser igual a f(x0,0)=0. Para el calculo de este limite lo traté como un limite de una sola variable.
Observé que en gral el limite da divergente, aunque en el caso x0=0 el resultado es 0, por lo que la función sería continua en el (0,0) pero no en los demas puntos de la forma (x,0). No se si es correcto lo que hice o deberia haber hecho algo distinto.
Saludos.