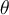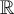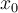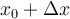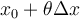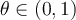Hola,
Tengo una duda en la igualdad 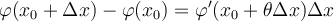 . Entiendo que
. Entiendo que 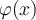 sea la intersección de
sea la intersección de 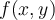 con el plano
con el plano 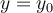 porque es lo que nos interesa estudiar al estarnos moviendo sólo en
porque es lo que nos interesa estudiar al estarnos moviendo sólo en 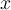 , lo que no entiendo es el término
, lo que no entiendo es el término 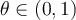 , no sé si es variable o constante. Asumo que es parte del teorema, pero no logro interpretar su función. Gracias.
, no sé si es variable o constante. Asumo que es parte del teorema, pero no logro interpretar su función. Gracias.
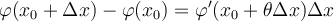 . Entiendo que
. Entiendo que 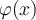 sea la intersección de
sea la intersección de 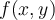 con el plano
con el plano 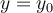 porque es lo que nos interesa estudiar al estarnos moviendo sólo en
porque es lo que nos interesa estudiar al estarnos moviendo sólo en 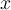 , lo que no entiendo es el término
, lo que no entiendo es el término 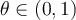 , no sé si es variable o constante. Asumo que es parte del teorema, pero no logro interpretar su función. Gracias.
, no sé si es variable o constante. Asumo que es parte del teorema, pero no logro interpretar su función. Gracias.Saludos