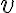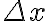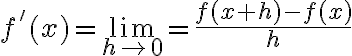Hola, en la clase 28 y en algunos momentos de las clases anteriores me confunde la interpretacion del h con el que trabajamos en derivadas direccionales y en el repaso de Taylor.
Entiendo que funciona para las definiciones pero no logro ver (si existe) una interpretación. Si me lo pueden intentar explicar de alguna manera les agradezco.
Saludos.
Hola Facundo. Una interpretación que podés hacer de la variable 
es que
es el límite del incremento medio de la función al moverse una proporción del vector 
. Algo así como una versión infinitesimal del cociente 
, donde, si tomamos vectores de módulo 1, es precisamente 
.
Fijate además que en la definición de derivada (en una variable) tenemos
donde, al tener una sola dimensión no indicamos vector dirección ya que puede interpretarse que tenemos una única dirección posible, y asumimos que el vector tiene módulo 1.
En el caso de Taylor no me queda de todo clara cuál es la duda, pero si querés contame mejor y la seguimos por acá. Saludos.