Foro Práctico 7.

Mauricio, todo bien?

La idea en este ejercicio es más bien trabajar con la ecuación de Laplace, te explico:

En estos casos es conveniente definir el campo intensidad magnética H, el cual es igual a 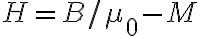$H= B/\mu_0 -M$. 

Este campo, cuando no tenés corriente que no sea de magnetización, se puede ver que viene de un potencial (ya que 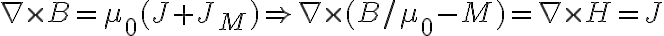$\nabla \times B = \mu_0(J+J_M) \Rightarrow \nabla \times (B/\mu_0-M) =\nabla \times H= J$), por lo tanto $\nabla \times H= 0$.

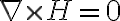Por último, como la magnetización es uniforme, 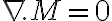$\nabla . M= 0$, en definitiva, 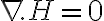$\nabla . H= 0$ y llegamos entonces a que el potencial 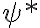$\psi*$ cumple la ecuación de Laplace.

Una vez visto esto y dada la simetría del problema, es sencillo ver que se reduce a resolver la ecuación de Laplace y "pegar" soluciones, como se había visto en la parte de electrostática.

Intentá por ahí y cualquier cosa volvé a preguntar! Igual este ejercicio se va a trabajar el Jueves en el práctico de Guzmán.

Suerte!