Hola, tengo una duda sobre cómo resolver este ejercicio. Al principio arranqué a mirar el problema por el lado de que sé que se cumple Rot(H)=0 fuera de la barra, y en ese caso podría escribir el H como el opuesto del gradiente de un potencial. (Fuera de la barra). Repasando las clases anteriores, vi que el profesor de teórico (de openfing) habló de que ese enfoque no era el que íbamos a dar. Cuál sería el método más adecuado al curso para resolver este ejercicio? Sería Mirando el vector A? y Calcular B a partir del Rotor de A?
Por otro lado, no estoy seguro sobre que sistema de coordenadas utilizar ya que tengo la magnetización M según k pero no sé si está del todo correcto usar coordenadas cilíndricas. El ejercicio pide el campo lejos, en este caso sería parecido al campo de un dipolo?
La idea de este ejercicio es considerar que el campo lejano de la barra se va a parecer al de un dipolo magnético. Así que lo primero que habría que hacer es hallar el momento dipolar magnético de la barra. Y luego el campo magnético de este dipolo.
Respecto a las coordenadas, la solución que aparece al final del práctico está escrita en coordenadas esféricas. También la figura del ejercicio te muestra r y θ de coordenadas esféricas. Así que convendría trabajar en estas coordenadas. Para escribir el momento dipolar se va a precisar el versor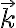 
, pero este se puede escribir en los versores de coordenadas esféricas.