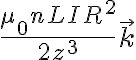hola intente demostrar que el campo lejos del solenoide es lo que dice la letra y tengo por ahora el campo en una espira que no se si esta bien, lo seguí de la clase de consulta del practico 7. y no se como sacar el campo que genera todo el solenoide.
el campo de una espira dio
En tu resultado no entiendo que es la componente según er. ¿Ese es el er de coordenadas cilíndricas? Eso no puede ser porque el ejercicio pide el campo en un punto del eje, y en esos puntos no está definido el versor er de coordenadas cilíndricas. En los puntos del eje el campo es solo según el versor k.
El campo del solenoide se obtiene como el campo de N espiras, y ese resultado ya se calculó en el Ejercicio No 6 del Práctico 6. Da:
![\frac{ \mu_0 N I R^2 }{2 \sqrt[]{R^2 + z^2}^3 } \vec{k}](https://eva.fing.edu.uy/filter/tex/pix.php/61110f80666f2a3bf39b00b849e723c7.png "\frac{ \mu_0 N I R^2 }{2 \sqrt[]{R^2 + z^2}^3 } \vec{k}")
Luego si n es el número de espiras por unidad de longitud, entonces N = nL y si estamos muy lejos de la espira, R << z. entonces queda:
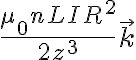
El campo de la barra se halla evaluando el resultado de la parte a en θ = 0.