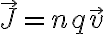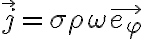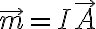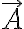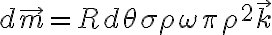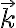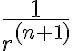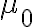ElecMag: Ej 10

Hola, buenas.
No entiendo mucho como utilizar la sugerencia de este ejercicio.

Sugerencia: Integre las contribuciones de momentos elementales (debido a espiras de ancho diferencial), luego de expresar la carga en rotación como una densidad superficial de corriente J.

1) No tengo muy claro como obtener el J que me habla. No entiendo como lograr expresar la carga en rotación como una densidad superficial de corriente. (No entiendo con seguridad como tomar esas espiras)

2) Luego de obtenido el J, la definición que tengo de momento magnético es: $gif.latex?%5Cvec%7Bm%7D%3DI%5Coint%20%5Cfrac%7B%5Cvec%7Br%7D%5Ctimes%5Cvec%7Bdr%7D%7D%7B2%7D$ . Cómo puedo involucrar ese J en esta definición?. (Es la definición de m para circuitos). También se qué $gif.latex?I%3D%5Cint%20_%7BS%7D%5Cvec%7BJ%7D.d%5Cvec%7Bs%7D$ , pero cuál sería esa superficie?

3) Respecto a las condiciones de borde para la parte b, Cuando hago la diferencia de las componentes tangenciales de los campos magnéticos, tengo que B1,T - B2,T = I. Esa sería la corriente por una espira, de las nombradas en la sugerencia de la parte a?. Por otro lado, cómo puedo conocer el comportamiento de esos potenciales escalares magnéticos cuando r tiende a infinito o cuando tiende a 0? Según una solución que vi en los dos casos son constantes, pero no logro entenderlo. Cómo me aseguro de su existencia?

Re: Ej 10

de Ricardo Marotti - sábado, 24 de octubre de 2020, 19:38

Te respondo numerando las respuestas como tus preguntas:

1) La densidad de corriente para cargas en movimiento es $\vec{J} = nq \vec{v}$ (ver ec 7.4 del Reitz, Milford, Christy), donde n es la densidad de partículas (partículas por unidad de volumen) que tienen carga q, y $\vec{v}$ es la velocidad de estas partículas. Luego nq es la densidad de carga por unidad de volumen (no le llamo ρ, porque voy a guardar esta letra para la coordenada radial en coordenadas cilíndricas). En este caso tenemos una densidad superficial de carga σ. Luego la densidad superficial de corriente será $\vec{j} = \sigma \rho \omega \vec{e_ \varphi }$ , ya que $\rho \omega \vec{e_ \varphi }$ es la velocidad de la carga superficial escrita en coordenadas cilíndricas (orientando el eje de las coordenadas cilíndricas según la dirección de la velocidad angular). Como σ es densidad de carga superficial (en lugar de carga por unidad de volumen) queda una densidad de corriente superficial (es decir corriente por unidad de longitud).

2) El momento dipolar magnético para una curva plana es $\vec{m}=I \vec{A}$ (ver ecuación 8.84 del Reitz, Milford, Christy), donde I es la corriente que circula por la curva y $\vec{A}$ es un vector perpendicular a la superficie encerrada por la curva, orientado por la regla de la mano derecha según la circulación de la corriente, y cuyo módulo es el área encerrada por la curva. Luego dividimos la superficie esférica en espiras circulares que subtiendan un ángulo dθ, siendo θ el ángulo polar de coordenadas esféricas. El ancho de estas espiras es R dθ. Luego la corriente que llevarán estas espiras es dI = R dθ σ ρ ω (densidad superficial de corriente por ancho de las espiras). Cada una de estas espiras tiene un área πρ². Luego la contribución al momento dipolar de cada una de estas espiras es $d \vec{m} = R d \theta \sigma \rho \omega \pi \rho^2 \vec{k}$ , siendo $\vec{k}$ el versor de coordenadas cilíndricas (dirigido según la velocidad angular). El momento dipolar total se calcula integrando en θ (de 0 a π) estos momentos diferenciales, teniendo en cuenta que ρ = R sen θ.

3) El potencial escalar magnético tiene que estar acotado en el centro de la esfera, porque en ese punto no hay ninguna singularidad (por ejemplo, no hay un dipolo magnético). Esto hace que los término de la forma $\frac{1}{r^{(n+1)}}$ sean todos nulos para el potencial en el interior del cascarón esférico. El potencial en el infinito tiene que estar acotado (no debe diverger) porque la distribución de corrientes está acotada en el espacio. Esto hace que todos los términos de la forma $r^n$ sean cero para el potencial fuera del cascarón esférico.

Las condiciones de borde en la frontera son que las componentes normales del campo magnético son iguales (porque el flujo a través de una superficie con forma de caja de píldoras que tiene una cara a cada lado de la frontera tiene que ser 0). Y de aplicar la ley de Ampere a una curva rectangular que tiene un lado a cada lado de la frontera (y los otros dos lados despreciables), la diferencia de los campos magnéticos tangenciales es $\mu_0$ por la densidad de corriente superficial (la hallada en la parte anterior.j = σ ρ ω = σ ω R senθ).