Foro Práctico 7

Hola Juan. Lo que ocurre con los conjuntos de nivel en funciones definidas por regiones depende de cómo sea la función (en particular las curvas de nivel podrían, o no, presentar discontinuidades)

Para estudiar los conjuntos de nivel en estos casos mi consejo es que en primer lugar tengas bien claro cuáles son las regiones, a nivel de dominio. Especialmente en casos donde esto no es explícito. Por decir un ejemplo de juguete, si tenemos la función 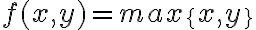$f(x,y) = max\{x, y\}$, podemos escribirla como

$f(x,y) = x$ si $x > y$ y $f(x,y) = y$ en caso contrario.

Es decir que las distintas regiones en el dominio son los semiplanos delimitados por la recta 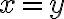$x = y$. En cada una de esas regiones la función responde a una expresión distinta (pero más sencilla digamos). Entonces Para cada una de esas regiones, estudiá los conjuntos de nivel de la expresión correspondiente como si fuesen funciones distintas. 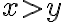En nuestro ejemplo, tendrías que trazar las curvas de nivel para la función $x$ en el semiplano $x>y$ y las curvas de nivel para $y$ en el semiplano $x \leq y$.

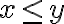Espero que el ejemplo sirva de guía. Otra opción un poco artificial que puede ayudar es pensar en algun ejemplo de función definida por regiones pero en una sola variable como para ejercitar el concepto en un terreno más conocido. Aunque los conjuntos de nivel en estos casos suelen quedar poco interesantes.

Saludos.