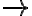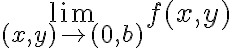Buenas! mi duda en este ejercicio era mas una cuestion teorica, queria saber si para calcular el limite cuando x tiende a 0 podria hacer algo analogo a lo que haciamos en calculo 1 cuando nos acercabamos por derecha o izquierda, pero manteniendolo para cualquier y, o sea no utilizar un valor de y especifico.
 existe, no basta con mirar que pasa al acercarse a
existe, no basta con mirar que pasa al acercarse a  por todas las rectas posibles. Deberías acercarte a
por todas las rectas posibles. Deberías acercarte a  por todas las curvas posibles, lo cual no es muy práctico que digamos y no es el enfoque que recomendaría para hallar un límite.
por todas las curvas posibles, lo cual no es muy práctico que digamos y no es el enfoque que recomendaría para hallar un límite. de modo que el límite de la función al acercar
de modo que el límite de la función al acercar 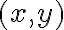 a dicho punto sea distinto en una u otra, entonces el límite en cuestión no existe.
a dicho punto sea distinto en una u otra, entonces el límite en cuestión no existe.Hola! Me parece que no me expresé muy bien en mi pregunta, a lo que me refería, más que a acercarme a un punto por una recta es a acercarme a una recta por puntos x e y cualquiera. Por ejemplo en el ejercicio 11 c de este practico tengo una recta en la que no se si mi función es contínua o no, entonces mas que a analizar caso por caso, que es imposible dado que una recta contiene infinitos puntos, sería calcular el límite para un y genérico acercandome a 0- en x, dado que la recta en la que desconozco la continuidad sería x=0 (donde la funcion cambia de expresión si voy por izquierda o derecha)
En resumen, mi pregunta sería si es correcto expresar el lìmite de la siguiente manera:
lim f(x,y) = y2
Ok, creo que ahora entendí mejor.
La respuesta es que la idea tiene cosas bien pero no es exactamente así. Recordemos que una función es contínua si es contínua en cada uno de sus puntos. Entonces para estudiar la continuidad de la función, estudiamos la continuidad en  , para todo punto
, para todo punto  del dominio.
del dominio.
Entonces en un ejercicio como el 11c) para estudiar continuidad en  podemos considerar tres situaciones:
podemos considerar tres situaciones:
- Cuando
 está en la región
está en la región 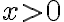 , es decir, cuando
, es decir, cuando 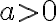
- Cuando
 está en la región
está en la región 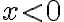 , o sea,
, o sea, 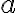
- Cuando
 está en la región
está en la región 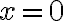 , es decir, cuando
, es decir, cuando 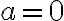
 es punto interior de la región donde la función está definida de una u otra forma. Así, en el caso 1 por ejemplo la función es contínua porque la expresión
es punto interior de la región donde la función está definida de una u otra forma. Así, en el caso 1 por ejemplo la función es contínua porque la expresión 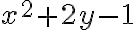 lo es.
lo es. de dicha región, sabemos que
de dicha región, sabemos que 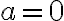 por lo que el punto es
por lo que el punto es 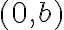 , donde
, donde  es arbitrario pero fijo. Por lo tanto, el límite que querés estudiar es
es arbitrario pero fijo. Por lo tanto, el límite que querés estudiar es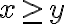 , entonces el límite será
, entonces el límite será 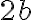 (porque uso la primer expresión) Y si me acerco por una curva incluída en la región
(porque uso la primer expresión) Y si me acerco por una curva incluída en la región 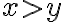 el límite será
el límite será 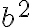 .
. es de tal modo que
es de tal modo que 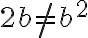 , la función no será continua en
, la función no será continua en 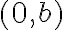 ¿Y si caso
¿Y si caso 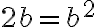 ? Se puede probar que en esos puntos la función sí es contínua. Es un ejercicio interesante, y básicamente consiste en usar la definición de continuidad para, a partir del hecho de que en cada una de los interiores de las regiones es contínua, encontrar un entorno adecuado para verificar la definición de continuidad en los
? Se puede probar que en esos puntos la función sí es contínua. Es un ejercicio interesante, y básicamente consiste en usar la definición de continuidad para, a partir del hecho de que en cada una de los interiores de las regiones es contínua, encontrar un entorno adecuado para verificar la definición de continuidad en los  adecuados.
adecuados.