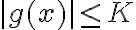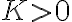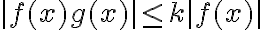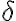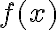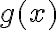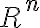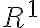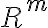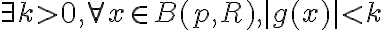Hola, no logro entender bien lo que estoy buscando demostrar en esta parte. Me confunde un poco el punto P, no entiendo si forma parte del dominio, del codominio o de ambos. Como hacemos el limite con x tendiendo a P, puedo asumir que esta en el dominio, pero también dice que g esta acotada en una bola reducida de centro P, por lo que ahí P estaría en el codominio.
Además de eso tampoco logro entender la idea de la demostración, agradecería si me pudieran guiar.
Saludos.
Bien, el punto p estaría en el dominio de f como en el de g.
La idea es probar que si tenes una función que tiene a cero en un punto y otra que está acotada ''cerca'' de ese punto, es decir, la tenes controlada, entonces el limite de la multiplicación es cero.
Como al tomar límite, en algún momento estas ''cerca'' del punto p, por lo que vas a tener 
para algun 
entonces 
y ahi seguís.
final fuera el mínimo entre el que usa 
para tender a 
y el 
en el que está acotada 
, porque si el de fuera más grande que el no estaría definida en esa bola reducida. ¿Estoy bien en esto?
a 
(la hipótesis no lo aclara, llegué a pensar que íbamos de a 
). Habitualmente si en un ejercicio algo se refería al dominio decía algo del tipo " definida en bla bla bla". Agradezco si me pueden aclarar esto.Buenas!
Está perfecto el planteo del y el , efectivamente tiene que ser el mínimo entre los dos.
Por otro lado cuando dicen "g es una función acotada en una bola reducida de centro p" refiere a que si tomas el dominio de la función y ves todas las imágenes de esa bola reducida, ese es un conjunto acotado, dicho de otra forma: 
Saludos!