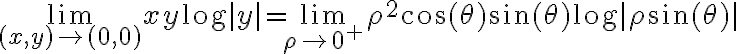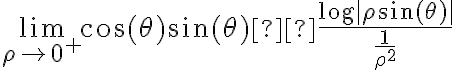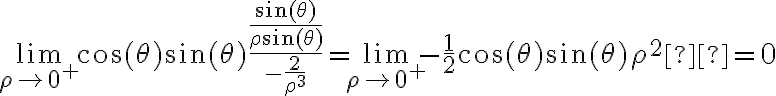No se me ocurre cómo encarar el ejercicio, intenté por coordenadas polares pero sigo con la indeterminación.
Buenas!
Pasar a coordenadas polares es útil en este caso, arrancaste bien, vemos como seguir.
Para llegar a un resultado utilizando polares necesitamos obtener 0 por acotado, sino no podemos definir la existencia del límite. En este caso tenemos que 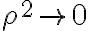 y por otro lado
y por otro lado 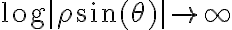 por lo que podemos pasar dividiendo como su inverso a
por lo que podemos pasar dividiendo como su inverso a 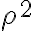 :
:
Ahora tenemos una indeterminación del tipo infinito sobre infinito y podemos aplicar L'Hopital:
Saludos!
Florencia
Hola Florencia, una consulta.
Tenía entendido que L'Hopital de momento era para una sola variable y que en polares seguimos teniendo 2 variables (aunque vayamos fijando distintos y llevando
y llevando 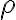 a
a  .
.
Sin embargo, en principio hice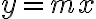 , sustituí en el límite, apliqué L'Hopital y me dió
, sustituí en el límite, apliqué L'Hopital y me dió 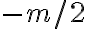 , por lo que el límite no existía porque dependía de
, por lo que el límite no existía porque dependía de 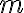 . Al ver la solución vi que estaba mal y no entendí por qué. Estoy entreverado la verdad.
. Al ver la solución vi que estaba mal y no entendí por qué. Estoy entreverado la verdad.
Eso sí, con la sugerencia de la solución sale sin problema.
Saludos y gracias
Tenía entendido que L'Hopital de momento era para una sola variable y que en polares seguimos teniendo 2 variables (aunque vayamos fijando distintos
 y llevando
y llevando 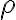 a
a  .
.Sin embargo, en principio hice
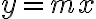 , sustituí en el límite, apliqué L'Hopital y me dió
, sustituí en el límite, apliqué L'Hopital y me dió 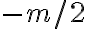 , por lo que el límite no existía porque dependía de
, por lo que el límite no existía porque dependía de 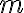 . Al ver la solución vi que estaba mal y no entendí por qué. Estoy entreverado la verdad.
. Al ver la solución vi que estaba mal y no entendí por qué. Estoy entreverado la verdad.Eso sí, con la sugerencia de la solución sale sin problema.
Saludos y gracias