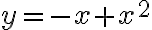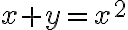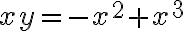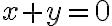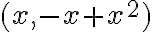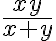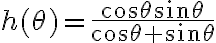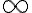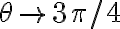5.c

5.c

de Maria Belen Santos Incerti -
Número de respuestas: 7

Hola, intentando hacer este ejercicio no encontré ningún camino para que el limite no me quede cero. Vi lo que dice Marcelo en las notas sobre este mismo ejercicio y lo entiendo. Pero de todas formas yo debería encontrar alguna sucesión para la que el limite no me de cero o verificarlo de alguna otra forma, pero no se me ocurre nada. Si me pudieran guiar en el razonamiento seria de mucha ayuda.

Gracias, saludos.

En respuesta a Maria Belen Santos Incerti

Re: 5.c

de Federico Carrasco Ferretti -

Tomate por ejemplo el la curva y=-x+x^2 y ahi x+y=x^2 y xy=-x^2+x^3 y como x tiene a cero te quedas con el de menor grado y ahi te queda pronto.

De donde se me ocurrio ese ejemplo, de acercarme al ''problema'' es decir al cero del denominador. 
En respuesta a Federico Carrasco Ferretti

Re: 5.c

de Mateo Molfino Ximenez -

El cero del denominador sería x+y=0 cierto? En que te fijas para acercarte a ese 0? Digo, porqué específicamente esa curva?

En respuesta a Mateo Molfino Ximenez

Re: 5.c

de Federico Carrasco Ferretti -

Si si, el cero del denominador es x+y=0. Pero si te moves por esa recta, la función es constante igual a 0.

En este caso como te piden el límite cuando tendes a (0,0), el ''problema'' estaría en (0,0), por lo que habría que encontrar una curva, por la que el límite si me muevo por esa curva sea distinto que moverme por la recta $y=-x$. 

Fijate que la curva (x,-x+x^2) tiende al (0,0) si x tiende a 0.

Porque elegí esa curva en particular, para que $xy$ fuera equivalente a $x+y$, nada más que por eso.
En respuesta a Maria Belen Santos Incerti

Re: 5.c

de Rafael Alejandro Ferreira Campanella -
En este ejercicio lo pase a polares y me quedó algo de la forma h(r).k(tita) lo cual tiende a 0.

Pero sabemos que el limite no existe, no da 0 para alguna curva, entonces ¿Por qué me da cero? ¿esto de h(r).k(tita) son limites direccionales?

¿No es que si g(r,tita) tiende al limite este existe?

tengo un mareo importante
En respuesta a Rafael Alejandro Ferreira Campanella

Re: 5.c

de Bernardo Marenco -

Hola. \displaystyle \frac{xy}{x+y} pasado a polares queda \displaystyle r\frac{\cos \theta \sin \theta}{\cos \theta+\sin \theta}, así que en este caso \displaystyle h(\theta) = \frac{\cos \theta \sin \theta}{\cos \theta+\sin \theta}. Fijate que lo demostrado en el ejercicio 4 pide que h sea una función acotada, lo que aquí no sucede ya que h se va a \infty cuando el seno y el coseno son opuestos, por ejemplo cuando \theta \to 3\pi/4. Por lo tanto, lo del ejercicio 4 no aplica en este caso.

Saludos
En respuesta a Bernardo Marenco

Re: 5.c

de Marcos Dura Sosa -
Buenas,

Mi duda con el ejercicio es que podemos confirmar que no existe el limite porque el limite en polares es distinto al limite y=0 no? Si fueran iguales no podriamos concluir nada o me equivoco?

Muchas gracias.
En respuesta a Marcos Dura Sosa

Re: 5.c

de Leandro Bentancur -
Buenas,

El límite direccional te da siempre 0, lo que no nos permite concluir nada. Para ver que no existe el límite podemos acercarnos con una parábola como explica Federico más arriba. También es útil el comentario de Bernardo sobre por qué no podemos utilizar la propiedad del ejercicio 4 (justo es un ejemplo de lo que te comentaba en la respuesta al otro ejercicio, de que la parte que depende de \theta no es acotada).

Saludos,
Leandro