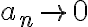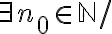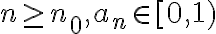Foro Práctico 4

Hola Melina. Para probar la convergencia de la serie 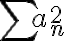$\sum a_n^2$ una estrategia posible es acotarla superiormente por otra que también converja (en este ejercicio es todo términos positivos así que sobreentiendo eso).

Dicha acotación no tiene por que ser para todos los términos de la sucesión, basta con que ocurra a partir de un cierto 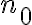$n_0$, tan grande como haga falta pero fijo. Luego para todo $n$ más grande que ese la cota debe valer.

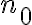Con esto en mente, podemos tomar la propia sucesión $a_n$ como cota, ya que como es convergente sabemos que tiende a cero y por lo tanto, a partir de un cierto $n_0$ elegido convenientemente, la sucesión $a_n$ será muy cercana a cero. En particular, menor a 1. Formalmente puedo decir pues que

Como $a_n \rightarrow 0$, $\exists n_0 \in \mathbb{N} /$ si $n \geq n_0, a_n \in [0,1)$.

¿Por qué elijo 1? porque si 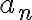$a_n$ tenemos que 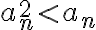$a_n^2 < a_n$ (estoy multiplicando por un número menor a 1, no negativo). Y en consecuencia, para todo 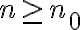$n \geq n_0$ vale que 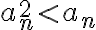$a_n^2 < a_n$, con lo cual controlamos el término principal de la serie que estamos estudiando por una que sí converge.

Espero se haya entendido mejor ahora, si no la seguimos.

Saludos.