En esta parte no se como darme cuenta que series debo usar para utilizar el criterio de equivalencia. La parte a la pude hacer pero en la parte b y c se me complica entender a que serie corresponde bn, la serie que utilizare para comparar con an.
Hola Federica
Cuando tenés polinomios es bastante sencillo: al igual que con las funciones polinómicas en cálculo 1, en el infinito los términos del numerador y denominador que importan son los de mayor grado. Podés probar que en la parte b el término
de la serie es equivalente en el infinito a 
.
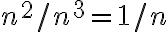Para la parte c), manipulando un poco la expresión, te va a servir recordar que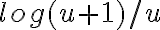
tiende a 1 cuando 
tiende a 0. Fijate si podés con esto, si no escribí.
Saludos!
Cuando tenés polinomios es bastante sencillo: al igual que con las funciones polinómicas en cálculo 1, en el infinito los términos del numerador y denominador que importan son los de mayor grado. Podés probar que en la parte b el término
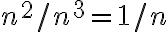de la serie es equivalente en el infinito a .Para la parte c), manipulando un poco la expresión, te va a servir recordar que
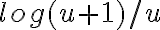tiende a 1 cuando tiende a 0. Fijate si podés con esto, si no escribí.Saludos!
Genial muchas gracias Favio!
En la parte b me queda que el limite es 1, por ende, según este criterio tienen el mismo comportamiento ambas series. Pero cuando averiguo si converge o diverge me da 0, por lo tanto las series convergen pero en la solución dice que divergen.
Hola, exactamente: la serie que aparece en b) es equivalente a la serie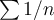 
. Pero esta serie diverge. Si bien 
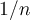tiende a 0, la suma diverge (acordate que 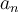tienda a 0 es una condición necesaria para que 
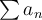sea convergente, pero no es una condición suficiente).
Hay varias formas de ver que la serie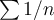 diverge (esta serie tiene nombre: serie armónica). En las notas por ejemplo se demuestra que esta serie diverge comparando con la serie 
que es una serie telescópica.
Pero hay otras formas tal vez más "intuitivas". Si te interesa en este link tenés un video que lo explica de otra forma y con una aplicación divertida (está en inglés pero podés ponerle subtítulos).
Saludos!
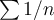. Pero esta serie diverge. Si bien 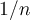tiende a 0, la suma diverge (acordate que 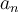tienda a 0 es una condición necesaria para que 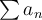sea convergente, pero no es una condición suficiente).Hay varias formas de ver que la serie
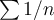diverge (esta serie tiene nombre: serie armónica). En las notas por ejemplo se demuestra que esta serie diverge comparando con la serie que es una serie telescópica.Pero hay otras formas tal vez más "intuitivas". Si te interesa en este link tenés un video que lo explica de otra forma y con una aplicación divertida (está en inglés pero podés ponerle subtítulos).
Saludos!
Entendí, muchas gracias Favio!