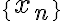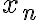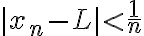Hola a todos.
Tengo una consulta sobre la demostración del directo en el siguiente ejercicio:
En la parte que dicen que L "además es la menor de las cotas superiores" se basa plenamente en la definición de supremo, ¿verdad?
La otra duda es ¿qué razonamiento utilizan para decir que existe esa sucesión convergente?
El recíproco se entiende muy bien.
Muchas gracias y disculpen las molestias.