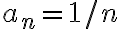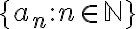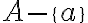Hola, necesito una mano con esta parte del Ejercicio.
Cuando lo fui a resolver, escribí que no existe una sucesión ya que por las notas del Teórico de Sucesiones (Página 19, Ejemplo 2) dice que los Naturales no tienen punto de aglomeración, y la Parte b) de este ejercico me pide dicha sucesión cuyos puntos de aglomeración sean estos Naturales.
Me recorrí el foro y vi lo que comentaron y las ideas que escribieron, así que me estoy equivocando al traducir los apuntes y no visualizo en que.
Agradezco respuesta.
Saludos.