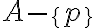Hola, hice el ejercicio pero no se si esta bien echo. O si basta lo que puse para demostrar el ejercicio, adjunto lo que puse.
"Si la bola fuese cerrada los puntos frontera estarian incluidos en el la bola, entonces esta no podria ser un conjunto abierto, ya que no todos sus puntos son interiores y por esto, la bola tiene que ser abierta para que sea un conjunto abierto"
Saludos y muchas gracias por sus respuestas
Diego : )
Hola Diego. Discrepo en el punto de partida de tu demostración: "Si la bola fuese cerrada..." (y a continuación demostrar por qué no puede pasar)
El problema con eso es que lo que estarías demostrando es que la bola no es cerrada. Pero eso no quiere decir que sea abierta. Un conjunto puede no ser abierto ni cerrado.
Lo que tenés que probar es que todo punto de 
es interior (al propio ). Y como ya sabés que 
es abierto sabes que dichos puntos son interiores a . La cosa es asegurar que puedas encontrar una bola contenida no sólo en sino en .
Otra idea es aprovechar (y escribir un poco mejor) tu razonamiento de los puntos frontera. Podés acomodar tu argumento por absurdo cambiando la afirmación inicial de "Si la bola (pichada) fuese cerrada" por un "Si la bola (pinchada) no fuese abierta", que es la negación literal de lo que queremos probar.
Fijate si te sirve alguna de estas ideas y si te animás mostranos después cómo te quedó escrita la prueba.
Saludos.