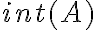Buenas, creo que logré comprender la idea de la demostración pero no siento que los argumentos que de sean del todo válidos y hay una parte que no se como justificar, además de con el dibujo.
Adjunto lo que hice para que me puedan ayudar.
Gracias, saludos!
Hola Iván. Tengo un par de observaciones sobre tu prueba.
La primera es con respecto al ítem que decís no saber justificar (lo de la frontera del interior). Lo que pasa ahí es que la afirmación en general no es cierta, pensá por ejemplo en un conjunto 
que tenga puntos aislados.
Igual podés probar el resultado sin usar aquella afirmación. Básicamente querés probar que todo punto de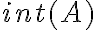 
es interior a 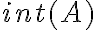. es decir que dado un punto 
genérico interior a deberías poder construir una bola centrada en él, toda formada por puntos interiores (tené en cuenta que sabemos que es interior a ).
Otra opción sería probarlo por absurdo, quedaría un argumento más parecido al que planteaste vos.