Dejo este hilo abierto, con la intento de seguir con Marcelo Fiori la consulta por dicho ejerció 1.c comenzando en la clase de consulta.
La parte problemática es encontrar el alfa que cumple ![\alpha (|x| + |y| ) \leq \sqrt[]{x^2 + y^2 }](https://eva.fing.edu.uy/filter/tex/pix.php/4d427ef5502044588c7587395d7e1090.png "\alpha (|x| + |y| ) \leq \sqrt[]{x^2 + y^2 }")
Saludos
Daniel
Hola Daniel. Voy a tirar un aporte al hilo pero de manera de dejarlo todavía abierto porque me parece súper interesante la discusión.
La idea que propongo, en primer lugar, es interpretar geométricamente qué es lo que tienen en ambos lados de la igualdad. Noten que hay un triángulo rectángulo subyacente ahí, con catetos que miden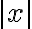 
e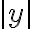 
y la hipotenusa 
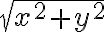(en particular, esta observación hace que sea bastante fácil hallar la otra constante 
).
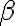Con esa consideración geométrica, les recomiendo buscar algo así como el "peor caso": ¿Cómo tienen que ser 
e 
para que la hipotenusa sea lo más chica posible, comparada a la suma de los catetos?