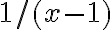 pero no logro entender porque
pero no logro entender porqueGracias
Hola Rodrigo. Ojo que esa equivalencia aplica en un entorno de 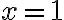 . Para entenderla, tené en cuenta que
. Para entenderla, tené en cuenta que
Como el denominador se anula en ambos extremos de integración, corresponde separar la integral en dos tramos. Para hacerlo igual que las soluciones, empecemos por mirar un tramo que contenga al extremo superior, por ejemplo integrar entre 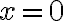 y
y 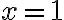
En ese intervalo, el factor 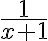 no tiene incidencia en el tipo de convergencia. De hecho podemos acotarlo inferiormente por 1/2 y decir
no tiene incidencia en el tipo de convergencia. De hecho podemos acotarlo inferiormente por 1/2 y decir
por lo que a los efectos de clasficar la integral, lo que nos interesa es clasificar la integral de 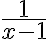 . Para el otro tramo puede usarse una idea similar y el factor que nos interesa es el otro. De todos modos como ya en este paso vemos que diverge no es necesario seguir.
. Para el otro tramo puede usarse una idea similar y el factor que nos interesa es el otro. De todos modos como ya en este paso vemos que diverge no es necesario seguir.
Espero se haya entendido. Saludos.