Ejercicio 10

Ejercicio 10

de Rodrigo Arakel Baliosian Garcia -
Número de respuestas: 1

Buenas, he realizado la parte de la integral de 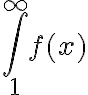 \int_{1}^{ \infty }{f(x)} , y me dio que era convergente, pero no logro sacar la convergencia de  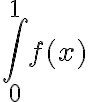\int_{0}^{1 }{f(x)} , como la podria resolver? 

Gracias.
En respuesta a Rodrigo Arakel Baliosian Garcia

Re: Ejercicio 10

de Veronica Rumbo -

Hola Rodrigo. Si integramos por partes como sugiere el ejercicio tenemos que

\int \log \left( 1 + \frac{a^2}{x^2}\right)dx = x\log \left( 1 + \frac{a^2}{x^2}\right) - \int \frac{2a^2}{x^2 + a^2}

siendo la última primitiva igual a 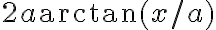2a \arctan(x/a).

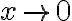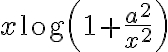Al considerar los extremos de integración 0 y 1, el único lugar no inmediato es el límite (con x \to 0) de x\log \left( 1 + \frac{a^2}{x^2}\right). Para resolver ese límite te sugiero considerar el cambio de variable 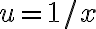u = 1/x, de modo que se convierte en un problema de órdenes de infinitos.