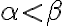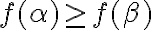Buenas, para usar este criterio tengo que tener una serie an y una integral impropia de f(t), donde f(t) es decreciente.
Para probar que f(t) es decreciente puedo utilizar un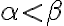 
y probar que f(
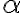<f
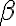). O también puedo derivar f(t) y fijarme a partir de cuando es decreciente? Y separar la integral impropia a partir de ese valor?
Gracias, saludos!
Así es. Tengo básicamente dos comentarios para reafirmar/ordenar lo que dijiste:
1- Para demostrar que una función es decreciente, podés usar la definición como dijiste (es decir tomar 
y ver que 
. O bien, si la función es derivable podés mirar el signo de la derivada.
2- Con respecto a partir la integral impropia en regiones: sí, se puede hacer. Y tené en cuenta que si una de las regiones resulta ser una integral no impropia, podés "olvidarte" de ella (a los efectos de determinar la convergencia. Si estás calculando cuánto vale la integral ahí sí vas a necesitar todo). Es lo mismo que hacemos cuando para clasificar una serie omitimos los primeros términos por conveniencia.