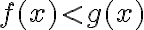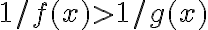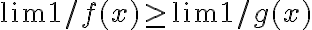Buenas, mi duda es la siguiente:
Si tengo dos funciones f(x), g(x), donde f(x)<g(x)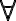 
x.
Entonces puedo hacer el inverso?de ser así quedaría de la siguiente manera? 1/f(x)>1/g(x).
Que pasaría si 1/f(x) y 1/g(x) tienden a infinito para algún x, entonces se seguiría cumpliendo la desigualdad? O sea el infinito de 1/f(x) es "mayor" al de 1/g(x).
Gracias, saludos!
Efectivamente, si 
, se cumple que 
.
Si dicha desigualdad se cumple para todo 
(o al menos para todos los en la zona del límite considerado), podés llevar ese argumento al límite, y tenés que 
Importante: Notar que cuando pasé al límite la desigualdad dejó de ser estricta. Es bastante fácil encontrar un ejemplo donde 
y 
sean como vos decís pero los límites sean iguales. Te invito a buscarlo.