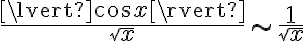Hola
El criterio de convergencia absoluta vale siempre. Lo que sucede en este caso es que no hay convergencia absoluta. Una forma de intentar usar convergencia absoluta sería algo así:
Para ver si 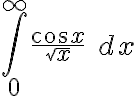 es convergente estudio la convergencia absoluta, es decir, si
es convergente estudio la convergencia absoluta, es decir, si 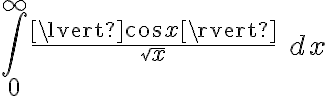 es convergente. Si logro probar esta última convergencia entonces vale la convergencia sin valor absoluto (eso dice el teorema).
es convergente. Si logro probar esta última convergencia entonces vale la convergencia sin valor absoluto (eso dice el teorema).
Esta última integral es convergente si y sólo si 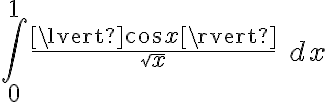 y
y 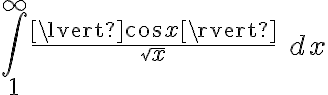 ambas convergen.
ambas convergen.
la integral impropia es de la misma clase que 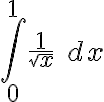 la cual es convergente. Por lo tanto
la cual es convergente. Por lo tanto 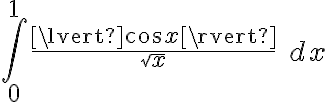 es convergente.
es convergente.
Ahora la segunda integral es lo problemático. 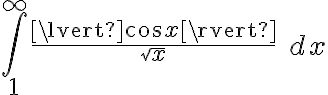 NO es convergente. Es por esto que
NO es convergente. Es por esto que 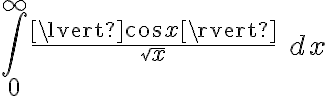 NO converge y por lo tanto
NO converge y por lo tanto 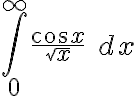 NO converge absolutamente... Es por esto (supongo yo) que en dicha clase no encararon por convergencia absoluta, porque no hay convergencia absoluta
NO converge absolutamente... Es por esto (supongo yo) que en dicha clase no encararon por convergencia absoluta, porque no hay convergencia absoluta