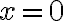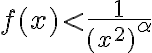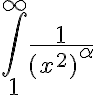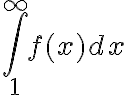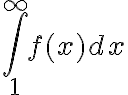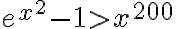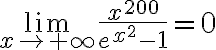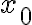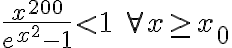CDIVV-2S: Ej. 7 parte b

Buenas! Quisiera consultar sobre este ejercicio.

En la b) por un lado llego (por comparación en el infinito con 1/(x^2)^α) a que α > 1/2 pero alrededor de 0, como por Taylor obtengo que es equivalente también a 1/((x^2)^α) concluyo que α < 1/2 para que converga. Entonces me queda que no hay alpha que sirva(? No entiendo, desde ya agradezco la ayuda

Re: Ej. 7 parte b

de Alejandro Bellati - viernes, 25 de septiembre de 2020, 14:15

Hola,

estoy de acuerdo con el equivalente en $x = 0$ . Ahora no entiendo muy bien la comparación al infinito que planteas.

¿Podrías explicar esa parte y discutimos?

Saludos

Re: Ej. 7 parte b

de Luciana Victoria Garcia Lombardi - viernes, 25 de septiembre de 2020, 14:50

Hola, yo lo pensé así: [e^(x^2) - 1] > x^2 y supuse que elevar ambos miembros a α (positivo, porque observé α que debía ser mayor a 0 para que el límite de f(x) dé 0) no me modificiaría la desigualdad. Luego, tomo los inversos y me queda la desigualdad a la que me refería; f(x) < 1/[(x^2)^α] y como esta función converge sii α >1/2 pensé que, por comparación, con f(x) pasaría lo mismo

Re: Ej. 7 parte b

de Alejandro Bellati - viernes, 25 de septiembre de 2020, 16:17

Estoy de acuerdo con todo lo que planteas. Pero con la conclusión final no. Lo que digo yo es que tener una desigualdad del estilo

$f(x) < \frac{1}{(x^2)^\alpha}$ solo te permite afirmar que si

$\int_1^\infty \frac{1}{({x^2})^\alpha}$ converge entonces

$\int_1^{\infty} f(x) dx$ converge. Pero! si

$\int_1^\infty \frac{1}{({x^2})^\alpha}$ diverge entonces no sé nada de la impropia de interes. Dicho de otra forma,

$\int_1^{\infty} f(x) dx$ y

$\int_1^\infty \frac{1}{({x^2})^\alpha}$ NO son equivalentes. Solo es cierto que la convergencia de la segunda implica la primera, pero no al revés.

En toda esta discusión obvie que

$f$ es no negativa.

---------------------------------------------------------------------------------------------------------------

Por otro lado, es cierto que

$e^{x^2} - 1 > x^{200}$ por lo menos a partir de un momento (a qué me refiero?, y por qué es cierto?)

Re: Ej. 7 parte b

de Luciana Victoria Garcia Lombardi - viernes, 25 de septiembre de 2020, 18:57

Ahh claro, muchas gracias por la ayuda! Lo de la exponencial mayor a la función potencia es por órdenes, no? O sea siempre se va a cumplir esa desigualdad para cualquier exponente porque nos importa lo que pasa en el infinito, y la exponencial crece mucho más rápido por ende en algún momento tiene que superar a la otra

Re: Ej. 7 parte b

de Alejandro Bellati - sábado, 26 de septiembre de 2020, 10:51

Lo de la exponencial es por órdenes sí. A mi me gusta decirlo así:

$\underset{x\to +\infty}{\lim} \frac{x^{200}}{e^{x^2} -1} = 0$ (por ordenes) y entonces, por definición de límite, existe $x_0$ tal que $\frac{x^{200}}{e^{x^2} -1} < 1 \ \forall x \geq x_0$ y despejando queda.