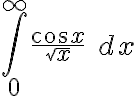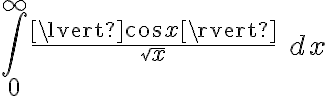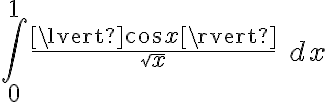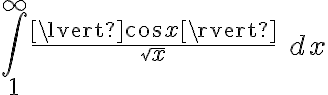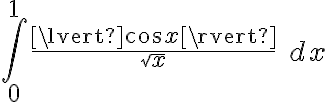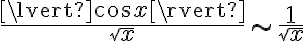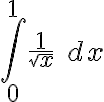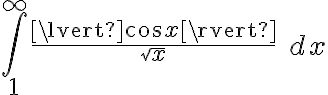Buenas tardes,
Cómo están?
Quería hacerles una consulta con respecto a este ejercicio. Estuve viendo este video: https://www.youtube.com/watch?v=OE9ZPaYw1Bo&t=12s y me queda bastante claro el método de resolución, pero tengo una duda. Porque no es posible aplicar por el Teorema de convergencia absoluta en la integral original que te da el ejercicio? Entiendo que es de segunda especie y que tiene los 2 "problemas" y quizá sea por eso, pero me gustaría confirmarlo por las dudas.
Gracias por su tiempo!
Saludo,
Ezequiel