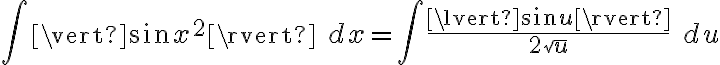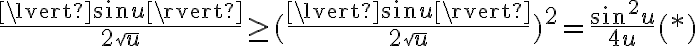Foro Práctico 5

Hola, te tiro algún pique que puede funcionar. No significa que es la única forma. Si consideras el cambio de variable 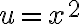$u = x^2$ entonces

$\int \vert \sin x^2 \rvert \ dx = \int \frac{\lvert \sin u \rvert}{2\sqrt{u}} \ du$

ahora este integrando es más conocido, fíjate que es con el que se trabaja en el ejercicio 4. Efectivamente diverge, para ver eso, una forma de hacerlo es:

$\frac{\lvert \sin u \rvert}{2\sqrt{u}} \geq (\frac{\lvert \sin u \rvert}{2\sqrt{u}})^2 = \frac{\sin ^2 u}{4 u} (*)$ siempre que $u$ sea grande

Ahora la integral 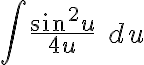$\int\frac{\sin ^2 u}{4 u} \ du$ va a diverger, y se puede ver usando partes. De hecho un compañero lo publicó en el foro (acá). 

Como verás te deje varios detalles para rellenar, como los límites de integración, porque vale 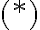$(*)$ y otras cosas. Intenta con esta pista (o por donde quieras), cualquier cosa volvé a preguntar que afinamos más.

Saludos