4(b)

4(b)

de Nicolas Fabian Seredni Silva -
Número de respuestas: 4

hola quería saber si todo lo que hice en el procedimiento es válido, (subo el ejercicio acá porque pesa más de 500kb).

graciass

En respuesta a Nicolas Fabian Seredni Silva

Re: 4(b)

de Alejandro Bellati -
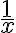Hola Nicolas, esta todo bien. Al final me quede buscando la conclusión igual. Lograste separar tu integral original en varios sumandos, todos convergiendo menos uno, el que tiene \frac{1}{x} solito. En conclusión tu serie original diverge.


Esta forma de hacerlo es la que sugerí en mi clase de hoy. Luego voy a subir un video haciéndolo de otra forma, por si te interesa.

Saludos
En respuesta a Alejandro Bellati

Re: 4(b)

de Diego Subeldia Loureiro -
Hola estimados, una consulta: no entiendo en el planteo del compañero por qué sen(x)^2=\frac{1}{2}-\frac{cos(2x)}{2}.
Y si estuviese ese vídeo resolviendo esta parte de otra forma me encantaría verlo.
Saludos!
En respuesta a Diego Subeldia Loureiro

Re: 4(b)

de Bernardo Marenco -
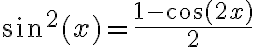Hola Diego. La identidad \displaystyle \sin^2(x) = \frac{1-\cos(2x)}{2} es una igualdad conocida. Una posible forma de demostrarla es usar la fórmula del coseno de la suma:

\displaystyle \cos(x+y) = \cos x \cos y - \sin x\sin y

(Una forma gráfica de probar esa igualdad se puede ver en esta imagen de Wikipedia).
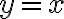Tomando y=x en esa igualdad se llega a 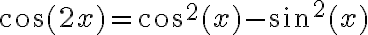\cos(2x) = \cos^2(x)-\sin^2(x). Y usando que 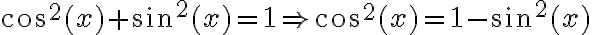\cos^2(x)+\sin^2(x)=1 \Rightarrow \cos^2(x) = 1-\sin^2(x) se llega a que 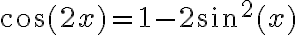\cos(2x) = 1-2\sin^2(x). La igualdad que queremos es una reescritura de esta última.

Sobre el video que decía Alejandro ahí: no se dónde está subido. Voy a buscarlo un poco más, si lo encuentro aviso por acá.

Saludos