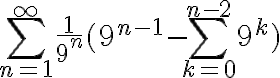Foro Práctico 4

Hola Juan. No logro darme cuenta como llegaste a esa expresión, pero puede escribirse de modo más simple.

Pensá en cada paso de la iteración, cuánta área estás sumando. En el primer paso (único cuadrado en el centro), se suma 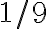$1/9$. Luego, en el segundo paso, pintás 8 cuadraditos de área 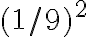$(1/9)^2$ cada uno (ya que el lado de cada cuadradito a pintar es $(1/3)^2$.

Más aún, en cada uno de esos 8 cuadrados sin pintar que rodean al del medio, tenés una situación que es similar a la del cuadrado original. Es decir que en la tercera iteración, en cada uno de los 8 cuadrados se pintarán 8 nuevos cuadraditos de área 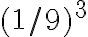$(1/9)^3$. Es decir que en la tercera iteración agregamos a la suma un área de $8^2\frac{1}{9}^3$.

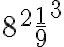En los siguientes pasos, ocurre algo similar. la cantidad de cuadraditos a sumar se multiplica por 8, y el área de cada uno se reduce en un factor 1/9. Esto debería darte una pista de cómo escribir la serie (si ves que no te sale, lo seguimos discutiendo). Después tendrás que hacer un pequeño ajuste para llevarla a la forma de una serie conocida cuya suma sabemos hallar.