CDIVV-2S: Ejercicio 2.a

Buenas, he estado intentando realizar el ejercicio 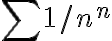$\sum{1/n^n}$ , por el criterio de comparación, pero no he encontrado otra serie 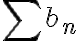$\sum{b_n}$ mas rápido. Como podría salir este ejercicio por comparación?

Gracias

Re: Ejercicio 2.a

de Veronica Rumbo - martes, 15 de septiembre de 2020, 17:16

Hola Rodrigo, te doy una pista. Fijate un par de cosas:

1- El criterio de comparación no tiene que ser literalmente para todos los términos de la serie. Basta con que encuentras una serie convergente cuyo término principal acote al tuyo a partir de cierto 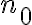$n_0$ fijo que podés elegir a conveniencia (lo mismo puede ser 1, 2, o 5millones, lo importante es que a partir de ese valor la acotación se verifique para todo $n$ )

2- La serie que tenés no es armónica pero "se parece". Capaz que podés ayudarte de alguna serie armónica para controlarla.

Saludos.

Re: Ejercicio 2.a

de Rodrigo Arakel Baliosian Garcia - miércoles, 16 de septiembre de 2020, 12:16

$n^n \geq n^2 \Rightarrow 1/n^2 \geq 1/n^n$ , como se que $1/n^2$ converge, entonces $1/n^n$ también converge. Mi razonamiento es correcto?

Re: Ejercicio 2.a

de Veronica Rumbo - miércoles, 16 de septiembre de 2020, 12:24

Así es. SImplemente agregaria que esas desigualdades que ponés son válidas para todo 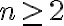$n \geq 2$ . A veces por brevedad en la escritura abusamos de notación y omitimos cuantificar las afirmaciones (sobreentendiendo que valen "para todo $n$ natural"). 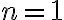En este caso me parece que vale la pena cuantificar explícitamente ya que la desigualdad no es cierta para todos los naturales (por ejemplo no lo es para $n = 1$ ), pero sí lo es a partir de un cierto valor fijo, que es lo que necesitamos.